Question

Точки A,B,C,D некомпланарны. На отрезках АС и ВС взяты соответственно точки М и N такие, что АМ:МС=ВN:NC=m:n. Найдите длину отрезка, заданного серединами отрезков АD и ВD, если MN=a.

Answer 1

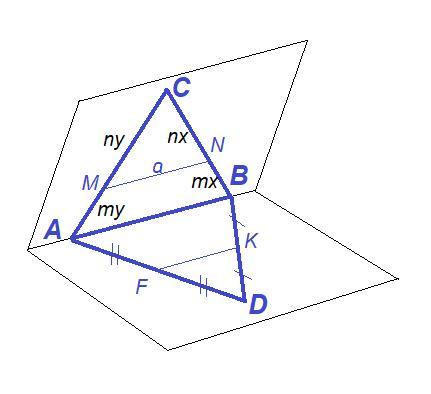
Дано:  D∉(ABC),  M∈AC,  N∈BC,

           АМ:МС=ВN:NC=m:n,  MN=a,

           F∈AD,  AF=FD,  K∈BD,  BK=KD

Найти:  FK

Решение:

По теореме Фалеса:

если   АМ:МС=ВN:NC=m:n,  то MN║AB.

⇒   ∠CMN = ∠CAB  как соответственные при MN║AB и секущей AC.

Значит, треугольники ABC и MNC подобны по двум углам (∠C - общий).

$\dfrac{AB}{MN}=\dfrac{AC}{MC}=\dfrac{BC}{NC}=\dfrac{m+n}n\\\\\\\dfrac{AB}a=\dfrac{m+n}n;\ \ \ \ AB=\dfrac{a\cdot (m+n)}n$

Рассмотрим треугольник ABD.

Точки F и К - середины сторон, значит, отрезок FK - средняя линия треугольника ABD, параллельная стороне AB. Значит, длина FK равна половине стороны АВ.

$FK=\dfrac{AB}2=\dfrac{a(m+n)}{2n}$

Ответ: $\boldsymbol{\dfrac{a(m+n)}{2n}}$