Предположим, что потребитель имеет доход в 3800 ед., цена товара А = 200 ед., а цена товара Б = 100 ед.
Найдите комбинацию товаров А и Б, находящуюся на бюджетной линии.
Ответы
Ответ:
(Товар Б; Товар А): (0;19) (36;1) (34;2) (32;3) (30;4) (28;5) (26;6) (24;7) (22;8) (20;9) (18;10) (16;11) (14;12) (12;13) (10;14) (8;15) (6;16) (4;17) (2;18) (0;19)
Объяснение:
Пусть по оси 0y будут товары А, на оси 0x будут товары Б
Для нахождения комбинаций товаров А и Б, находящейся на бюджетной линии:
1) Найдем крайние точки, когда весь доход потребитель потратит на один товар:
3800/200= 19 товаров может позволить себе потребитель, если потратит бюджет только на товар А;
3800/100= 38 товаров может позволить себе потребитель, если потратит бюджет только на товар А;
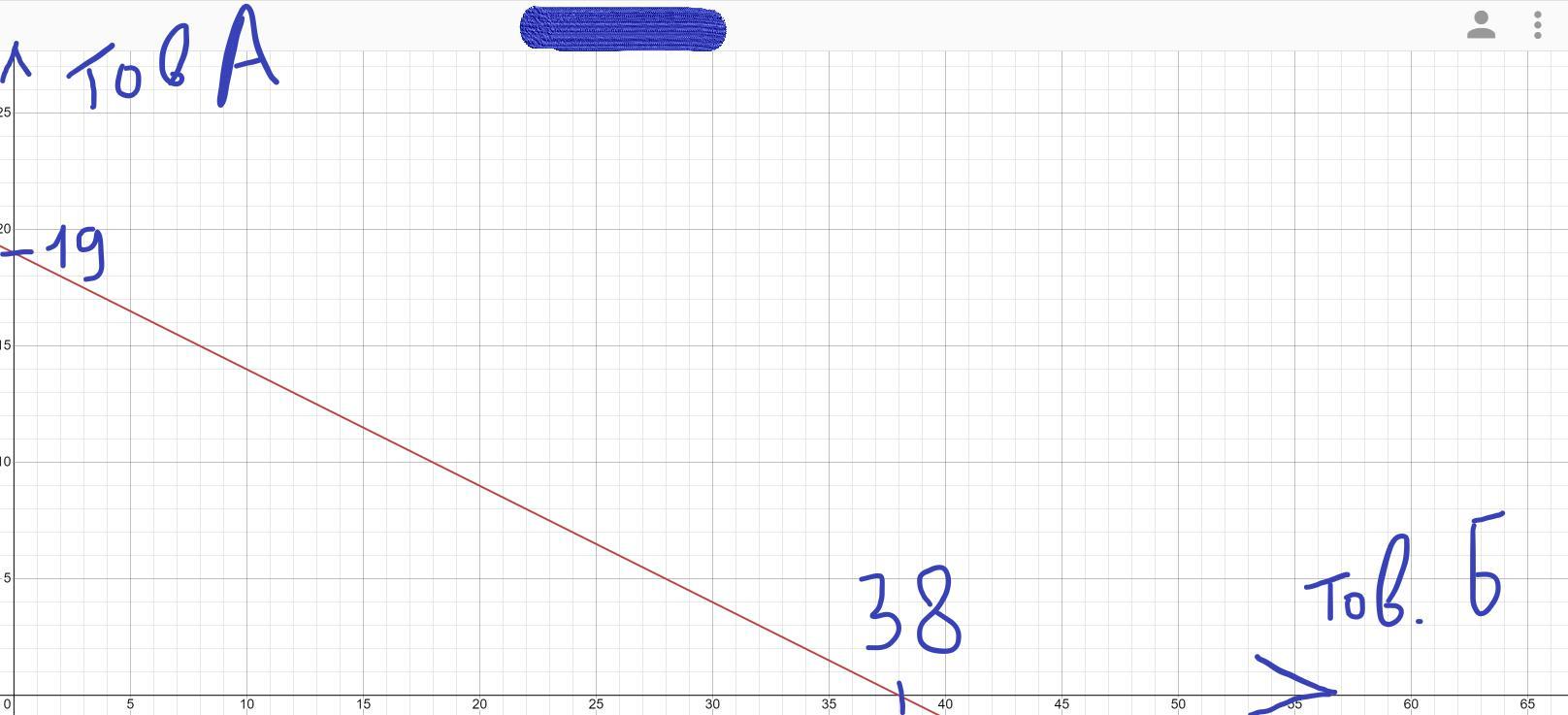
2) Теперь построим график и отметим на нем эти точки:
максимум А (0;19), максимум (38;0), соединим точки, так мы получили линию бюджетного ограничения. Цена 1 товара А = 2 товарам Б.
3) Понимаем, что функция графика имеет вид: Aу = 19 - 1/2Бх. Подставив любые значения в эти функции мы найдем все комбинации товаров А и Б, находящихся на бюджетной линии:
Если Б=6, то А = 16 товарам, так найдем все значения:
(Товар Б; Товар А): (0;19) (36;1) (34;2) (32;3) (30;4) (28;5) (26;6) (24;7) (22;8) (20;9) (18;10) (16;11) (14;12) (12;13) (10;14) (8;15) (6;16) (4;17) (2;18) (0;19)