Предмет: Геометрия,
автор: juliabarhatova787
Задание 4.
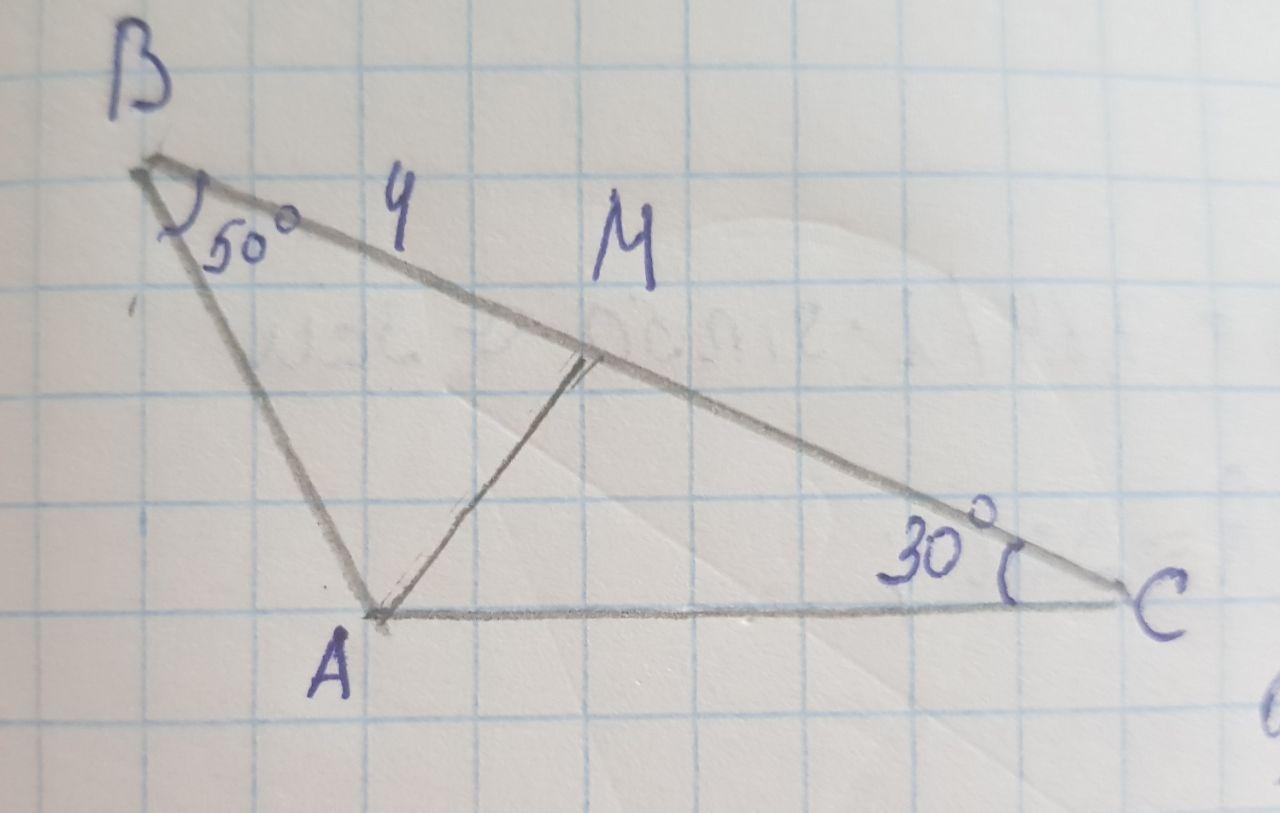
В треугольнике ABC проведена биссектриса AM. ∠ACB = 30°, ∠CBA = 50°, BM = 4 см. Выполните рисунок и найдите:
а) длину биссектрисы AM (10 баллов);
б) длину стороны AС (12 баллов);
в) радиус окружности, описанной около треугольника ABC (11 баллов).
Ответы
Автор ответа:
17
Ответ:
AM = 4 см; AC ~ 7,84; R ~ 3 см;
Объяснение:
a)
∠BAC =180-B-C =180-50-30 =100
∠BAM =∠BAC/2 =50 (AM - биссектриса ∠BAC)
∠BAM=∠B => △BMA - равнобедренный, AM=BM=4 (см)
б) ∠BМА = 180 - ∠В - ∠ВАМ = 180 - 50 - 50 = 100; ∠АМС смежный углу ∠ВМА, значит ∠АМС = 180 - ∠ВМА = 180 - 80 = 100.
АС ищем через теорему синусов, АМ/sin C = AC/sin AMC => AC = AM*sinAMC/sin C = 4 * sin 100/sin 30 = 8 * sin 100 ~ 8 * 0,98 ~ 7,84см
с) Радиус тоже через теорему синусов.
AC/sinB = 2R => R = AC / 2 * sin B = 7,84 / 2 * sin 50 ~ 3 см
Рисунок прикрепляю
Ответ: AM = 4 см; AC ~ 7,84; R ~ 3 см;
Выполнил Барановский Владислав
Можно пожалуйста лучший ответ)
Приложения:
siestarjoki:
Из треугольника BMA легко найти AB.
Из точки M опустим высоту/медиану. AB/2=4 cos50
^))))
а почему 7,84/2sin50 = 3 см....???
Здравствуйте, Юлия! В задании №4 можно было обойтись без использования приближенных значений. В остальном, задания выполнены верно, молодец! Желаем успехов в обучении:)
комментарий учителя
Спасииииииииииииииибо
Похожие вопросы
Предмет: Русский язык,
автор: KinCross
Предмет: Русский язык,
автор: vfrcbvsx
Предмет: Окружающий мир,
автор: Doget
Предмет: Английский язык,
автор: zsadirdinov007
Предмет: Алгебра,
автор: anastasiia40