ПОТРІБНО СРОЧНО! Обчислити координати точки перетину перпендикулярів, які проведені через середини сторін трикутника з вершинами: (2, 3), (0, −3), (6, −3).
Ответы
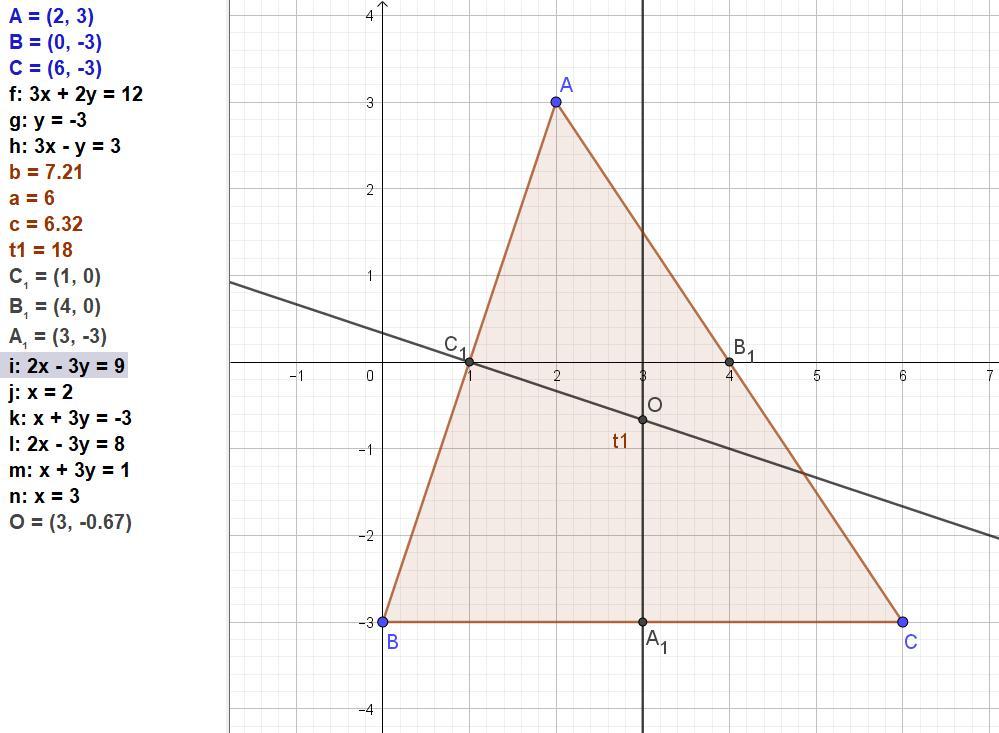
Дано трикутник з вершинами: A(2, 3), B(0, −3), C(6, −3).
Так как точки B(0, −3) и C(6, −3) имеют одинаковые ординаты, то это горизонтальная прямая, середина её - точка А1 = (B(0, −3)+C(6, −3))/2 =
= (3; -3).
Тогда срединный перпендикуляр стороны ВС - вертикальная прямая х = 3.
Угловой коэффициент стороны к(АВ) = Δу/Δх = (-3-3)/(0-2) = -6/-2 = 3,
середина её - точка С1 = (A(2, 3) + (B(0, −3))/2 =
= (1; 0).
Угловой коэффициент перпендикулярной прямой равен:
к1 = -1/к(АВ) =-1/3.
Уравнение перпендикуляра к середине АВ: у = (-1/3)х + b.
Для определения слагаемого b подставим координаты точки С1.
0 = (-1/3)*1 + b, отсюда b = 1/3, получаем у = (-1/3)х + (1/3).
Теперь можно определить точку О пересечения срединных перпендикуляров, так как абсцисса нам уже известна: х = 3.
Подставим в уравнение:
у = (-1/3)*3 + (1/3) = -1 + (1/3) = (-2/3).
Ответ: О(3; (-2/3)).