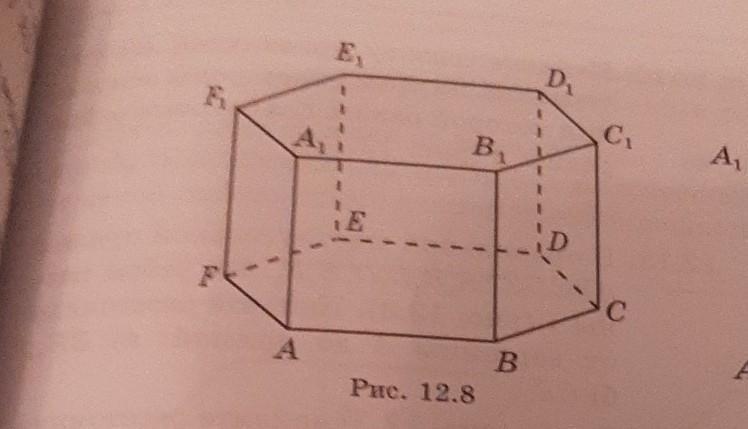
в правильной шестиугольной призмы ABCDEFA1B1D1E1 равны 1 (рис. 12.8).Найдите расстояние от вершины A до следующих плоскостей д) CDD1,; е) СЕЕ1; ж ) СFF1
Ответы
Объяснение:
В ПРАВИЛЬНОМ 6-УГОЛЬНИКЕ ВСЕ СТОРОНЫ РАВНЫ И КАЖДЫЙ УГОЛ РАВЕН 120°.
ТАК КАК ДАННЫЕ ПЛОСКОСТИ ПЕРПЕНДИКУЛЯРНЫ ОСНОВАНИЮ, ТО РАССТОЯНИЕМ ОТ ТОЧКИ ДО ПЛОСКОСТИ ЯВЛЯЕТСЯ ПЕРПЕНДИКУЛЯР, ПРОВЕДЁННЫЙ ОТ ДАННОЙ ТОЧКИ К ДАННОЙ ПЛОСКОСТИ.
д) меньшая диагональ правильного 6-угольника образует с его стороной прямой угол (свойство меньшей диагонали правильного шестиугольника), поэтому АС⏊СД, и АС – это расстояние от точки А до плоскости СДД₁
е) при пересечении меньшей и большей диагоналей правильного 6-угольника образуется 2 равных прямоугольных треугольника, поэтому диагонали ВF и СЕ перпендикулярны. Диагональ СЕ принадлежит плоскости СЕЕ₁ и расстоянием от точки А до этой плоскости является отрезок АМ, соответственно АМ⏊СЕ
ж) расстоянием от точки А до плоскости СFF₁ является перпендикуляр АН, при этом образуется прямоугольный треугольник АFН, в котором АН и FH – катеты, а AB – гипотенуза
РЕШЕНИЕ ВСЕХ ПУНКТОВ НА ФОТО!


