Предмет: Геометрия,
автор: Mishka1239
В конусе образующая равна l и наклонена к плоскости основания конуса под углом у. Сечная плоскость В проходит через вершину конуса и хорду АВ в его основе, при этом хорда АВ видна из центра основания конуса под углом а. Плоскость В образует с плоскостью основания конуса острый угол. 1) Изобразите сечение конуса плоскостью B и укажите вид полученного сечения. 2) Обоснуйте положение угла между плоскостью сечения и плоскостью основания. 3) Найдите периметр сечения. 4) Найдите площадь сечения.
Ответы
Автор ответа:
2
Ответ:
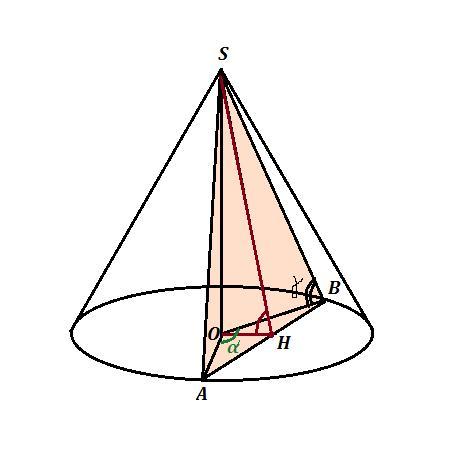
Дан конус, вершина в точке S . ∠SBO= , образующая SB=
.
Сечение - плоскость β - это плоскость АВS , ∠AOB=α .
1) Сечение АВS - равнобедренный треугольник, т.к. SB=SA= .
2) Угол между пл. АВS и пл. основания равен углу между двумя перпендикулярами , проведёнными в этих плоскостях к линии их пересечения . Такими перпендикулярами будут высота SH равнобедренного ΔАВS , основание которого , точка Н, является серединой стороны АВ , и перпендикуляр равнобедренного ΔАОВ ( АО=ВО=радиусу окружности ), основанием которого служит всё та же точка Н .
Угол между пл. АВS и пл. основания - это ∠SHO .
3) Периметр сечения ABS равен .
Из ΔАSО: ОА - радиус окр. R .
Из ΔАОВ по теореме косинусов
Из ΔSBO:
Приложения:
Mishka1239:
спасибо
очень помогли
писать долго геометрию
а что внизу красное
это вы через код писали ?
на рисугке красное - сечение
понял спасибо
писала через редактор формул LaTex , телефон читает текст ?
а как такой текст можно иначе написать, чтобы было читаемо ? разве что фото скинуть, но я фото не люблю
все нормально я зашёл через браузер и нормально
Похожие вопросы
Предмет: Русский язык,
автор: денис20043
Предмет: Русский язык,
автор: анрврр
Предмет: Русский язык,
автор: marina1111114
Предмет: Математика,
автор: betman1995
Предмет: Русский язык,
автор: wrestler51