Предмет: Алгебра,
автор: Аноним
Простейшие уравнения, решить подробно, без PhotoMath
Приложения:
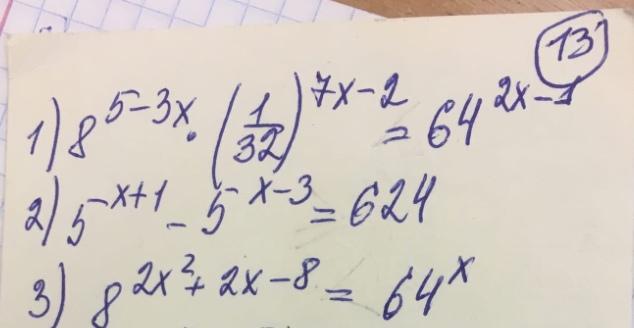
Ответы
Автор ответа:
1
Смотри.....................
Приложения:


MizoriesKun:
Неужели,))
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Артинян1
Предмет: Английский язык,
автор: аждваПТ
Предмет: Другие предметы,
автор: coolmolodcova
Предмет: Математика,
автор: margievaalinkapdto26
Предмет: Математика,
автор: Аноним