Question

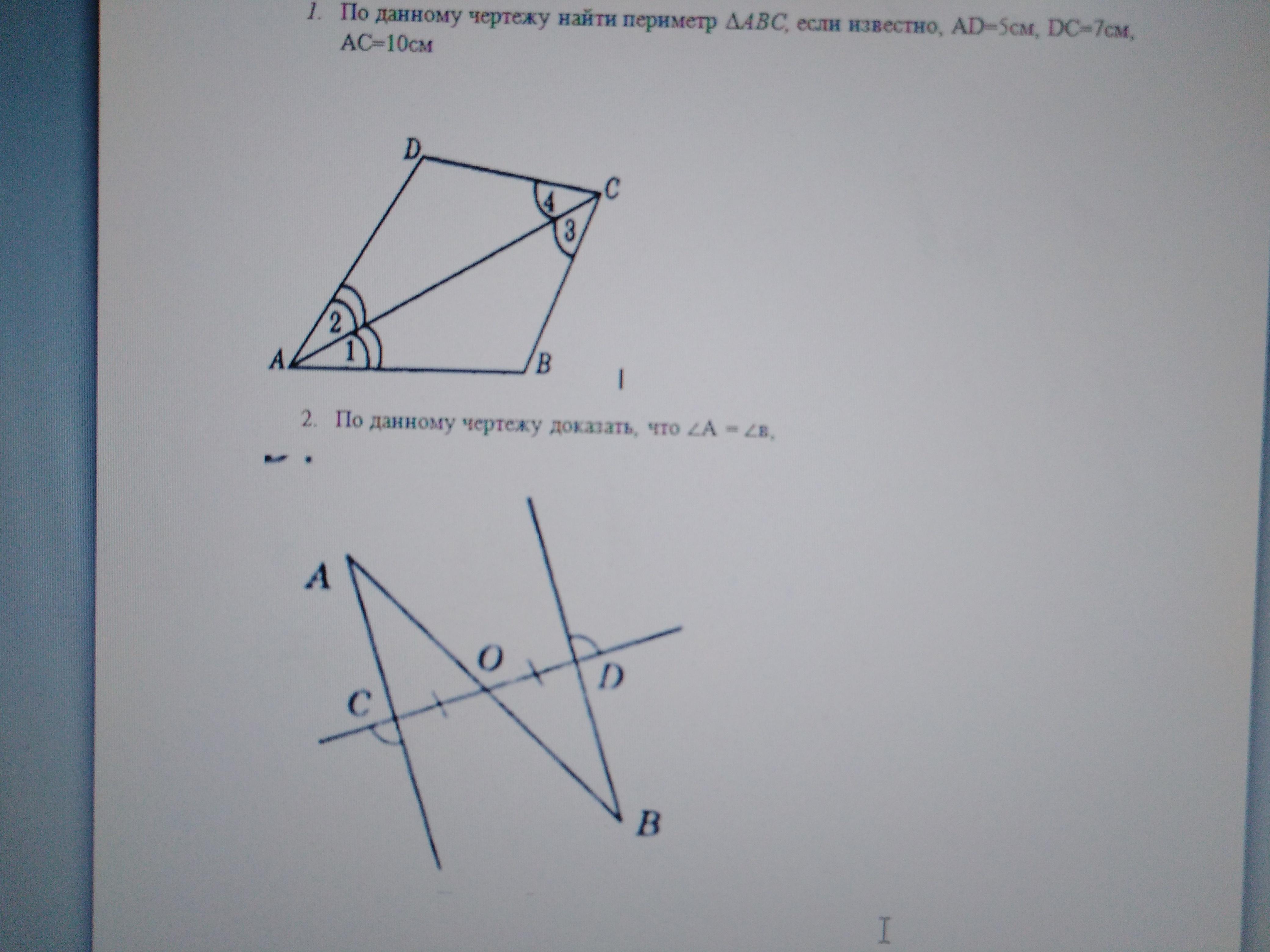
СРОЧНО, СРОК СДАЧИ ЗАВТРА!!!
ДАЮ 40 БАЛЛОВ!
Задания в файле.

Answer 1

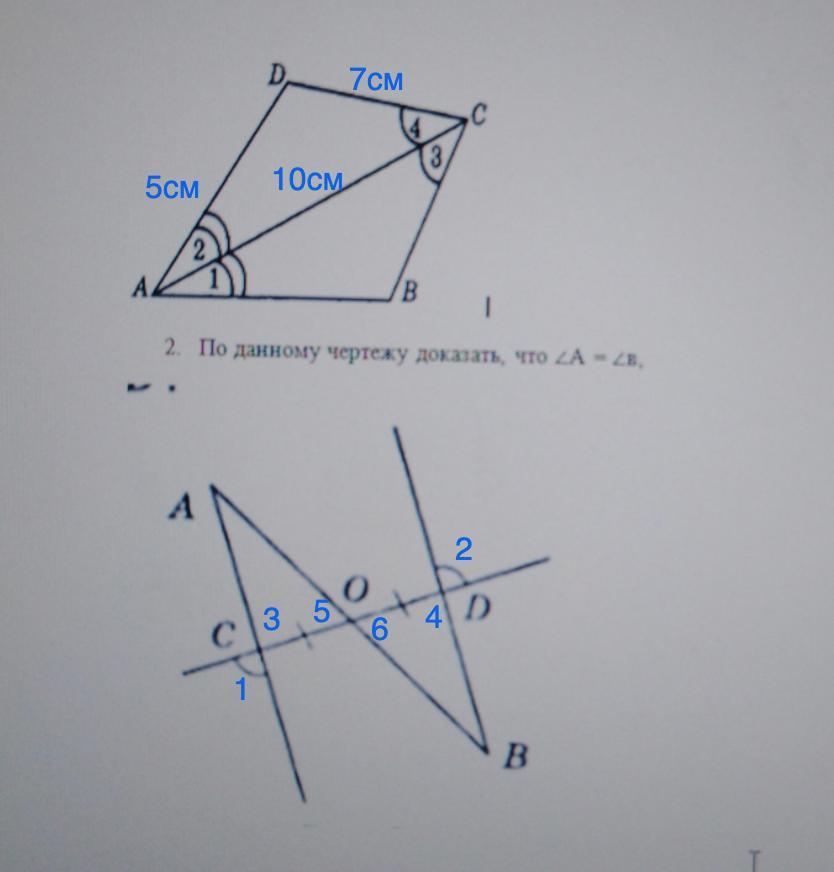
№1.

Рассмотрим Δ ABC, Δ ADC. ∠1 = ∠2 (по условию), ∠3 = ∠4 (по условию), AC - общая, ⇒ Δ ABC = Δ ADC (по II признаку, по стороне и двум углам). Но по условию AD = 5 см, DC = 7 см, AC = 10 см, ⇒ P (ΔADC) = 5+7+10 = 22 см, а т. к. Δ ABC = Δ ADC, то P (Δ ABC) = P (Δ ADC) = 22 см.

Ответ: P (ΔABC) = 22 см.

№2.

Т. к. ∠C = ∠D (по условию), а ∠ ACO = ∠C и ∠BDO = ∠D (вертикальные углы), то ∠ACO = ∠ BDO, ⇒ AC ║ DB (по накрест лежащим углам, секущая CD) ⇒ ∠A = ∠B (накрест лежащие, секущая AB).

чтд.

Answer 2

Объяснение:

1. Дано: ABCD.

∠1 = ∠2; ∠3 = ∠4

AD = 5 см; DC = 7 см; АС = 10 см.

Найти: Р (ΔАВС)

Решение:

Рассмотрим ΔАВС и ΔACD.

∠1 = ∠2; ∠3 = ∠4 (условие)

АС - общая.

⇒ ΔАВС = ΔACD. (по стороне и двум прилежащим к ней углам. 2 признак)

• В равных треугольниках соответственные элементы равны.

⇒ AD = AB = 5 см; DC = CB = 7 см.

• Периметр треугольника - сумма длин его сторон.

Р (ΔАВС) = АВ+ВС+АС = 5+7+10 = 22 (см)

2) Дано: ΔАСО и ΔODB.

CO = OD; ∠1 = ∠2.

Доказать: ∠А = ∠В

Доказательство:

Рассмотрим ΔАСО и ΔODB.

CO = OD (условие)

• Вертикальные углы равны.

⇒ ∠5 = ∠6 (вертикальные)

∠1 = ∠3; ∠2 = ∠4 (вертикальные)

∠1 = ∠2 (условие) ⇒ ∠3 = ∠4

⇒ ΔАСО = ΔODB  (по стороне и двум прилежащим к ней углам. 2 признак)

• В равных треугольниках соответственные элементы равны.

⇒ ∠А = ∠В