Question

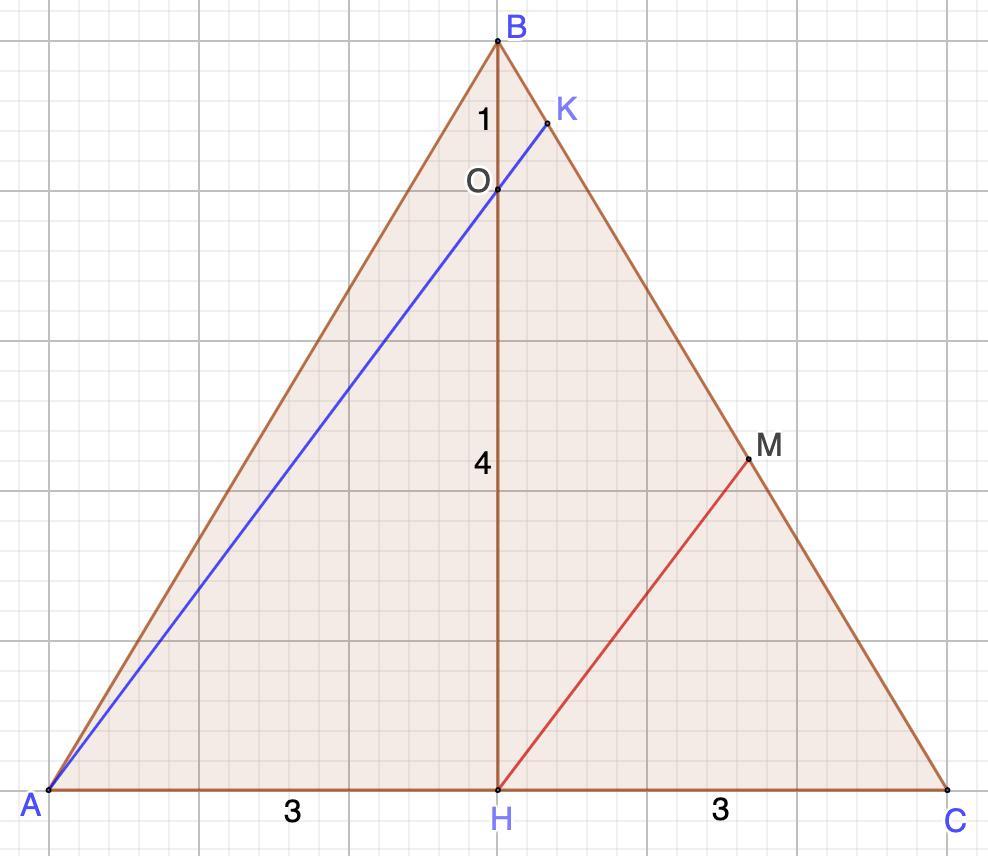
Дан равнобедренный треугольник АВС. Основание АС = 6. Высота ВН = 5. На высоте ВН взята точка О так, что ВО = 1. Прямая АО пересекает сторону ВС в точке К. Найдите АК. Прошу срочно помочь! Даю 30 баллов!

Answer 1

Ответ:

$AK=5\frac{5}{9}$

Объяснение:

Дано: ΔАВС - равнобедренный.

АС = 6; ВН = 5 - высота.

ОВ = 1.

АО ∩ ВС = К

Найти: АК.

Решение:

Проведем НМ || АК.

1. ОА = 5-1 = 4;

2. Рассмотрим ΔАВС - равнобедренный.

• В равнобедренном треугольнике высота , проведенная к основанию,  является медианой.

⇒ АН = НС = 6:2 = 3.

3. Рассмотрим ΔОВК и ΔНВМ.

ОК || НМ (построение)

• Лемма:  Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от данного треугольника ему подобный.

⇒ ΔОВК ~ ΔНВМ.

Составим пропорцию:

$\displaystyle \frac{OK}{HM}=\frac{BO}{BH} \\\\\frac{OK}{HM}=\frac{1}{5}$

Пусть ОК = х, тогда НМ = 5х.

4. Рассмотрим ΔНМС и ΔАКС.

НМ || АК (построение)

ΔНМС ~ ΔАКС (лемма)

Составим пропорцию.

$\displaystyle \frac{HC}{AC}=\frac{HM}{AK}\\\\\frac{3}{6} =\frac{5x}{AK} \Rightarrow AK=\frac{6*5x}{3}=10x$

5. Рассмотрим ΔAOH - прямоугольный.

По теореме Пифагора:

$\displaystyle AO^2=AH^2+HO^2=9+16=25\\\\AO=\sqrt{25}=5$

АО = АК - ОК = 10х - х = 9х

⇒ 9х = 5

$\displaystyle x=\frac{5}{9}$

Найдем АК:

$\displaystyle AK=10x=\frac{5}{9}*10 = \frac{50}{9} =5\frac{5}{9}$