Предмет: Математика,
автор: Keilsi
Найти область сходимости ряда
Приложения:
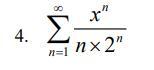
Ответы
Автор ответа:
0
Дан степенной ряд где
Найдем сначала радиус сходимости по формуле
Тем самым найден интервал сходимости
Остается исследование в точках 2 и - 2.
При x=2 получается ряд Этот ряд называется гармоническим. Как известно, он расходится (доказательство расходимости можно провести с помощью интегрального признака Коши).
При x = - 2 получается знакочередующийся ряд Он сходится по признаку Лейбница (члены ряда, взятые по модулю, монотонно стремятся к нулю). Поскольку ряд из модулей расходится. делаем вывод, что этот ряд сходится условно.
Вывод: областью сходимости является [-2;2).
Похожие вопросы
Предмет: Русский язык,
автор: настясоколова2
Предмет: Окружающий мир,
автор: SLAVABOXING123
Предмет: Русский язык,
автор: настясоколова2
Предмет: Другие предметы,
автор: Dadsuzan1243
Предмет: Русский язык,
автор: 7ж5к