Question

Помогите с геометрией, пожалуйста.
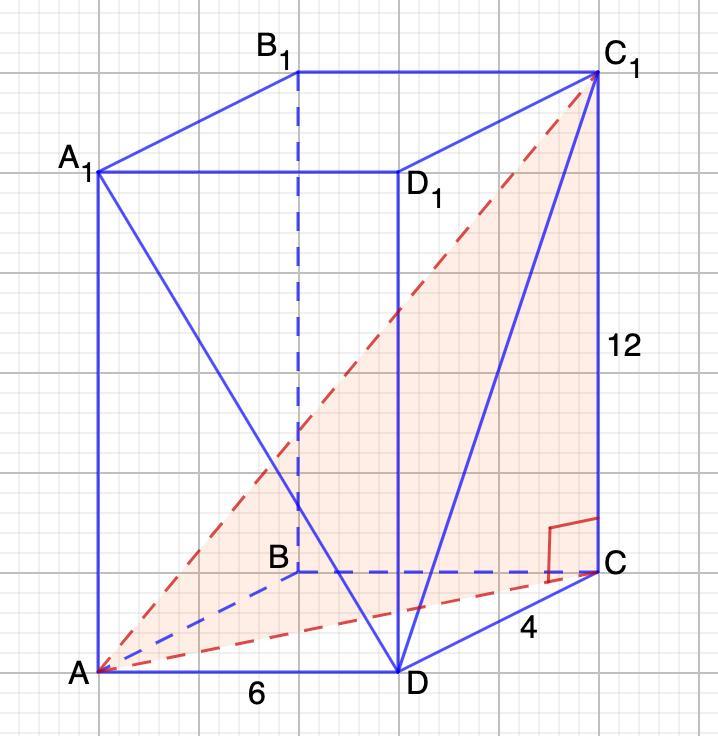
Рёбра прямоугольного параллелепипеда равны 4,6 и 12. Вычислите диагональ параллелепипеда и длины диагоналей боковых граней

Answer 1

Ответ:

A₁D=6√5; DC₁=4√10; AC₁=14

Объяснение:

Дано:

ABCDA₁B₁C₁D₁ - прямоугольный параллелепипед.

AD = 6; DC = 4; CC₁ = 12

Найти: A₁D; DC₁; AC₁.

Решение:

• Прямоугольный параллелепипед — это параллелепипед, у которого все грани прямоугольники.

1. Рассмотрим ΔAA₁D - прямоугольный.

По теореме Пифагора:

$A_1D=\sqrt{AD^2+AA_1^2}= \sqrt{6^2+12^2}=\sqrt{180}=6\sqrt{5}$

2. Рассмотрим ΔDC₁C - прямоугольный.

По теореме Пифагора:

$DC_1=\sqrt{DC^2+CC_1^2}=\sqrt{4^2+12^2}=\sqrt{160}=4\sqrt{10}$

3.Рассмотрим ΔACD - прямоугольный.

По теореме Пифагора:

$AC=\sqrt{AD^2+DC^2}=\sqrt{6^2+4^2}=\sqrt{52}$

4. Рассмотрим ΔАС₁С - прямоугольный.

По теореме Пифагора:

$AC_1=\sqrt{AC^2+CC_1^2}=\sqrt{52+144}=\sqrt{196}=14$