Предмет: Алгебра,
автор: sorokinazhanna2004
Решите уравнение под номером 5
Приложения:
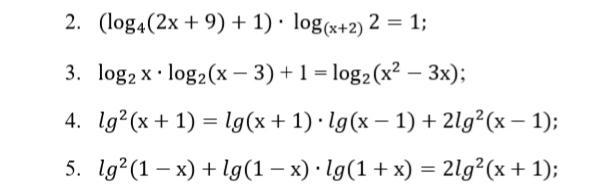
Ответы
Автор ответа:
1
Ответ:
Объяснение:
x=(-1-√5)/2∉(-1;1) не удовл.
x=(-1+√5)/2∈(-1;1)
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: нек18
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: kolpakova04
Предмет: Қазақ тiлi,
автор: vera1901
Предмет: Английский язык,
автор: olesia8888