Предмет: Математика,
автор: cw8zfv4tcf
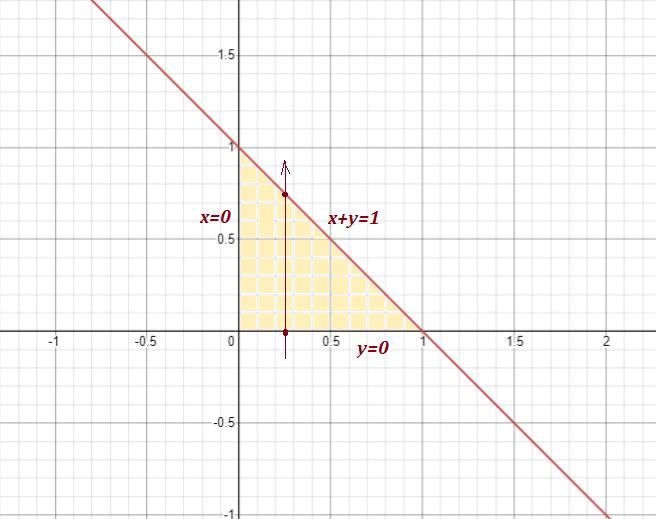
Вычислить двойной интеграл ydxdy по области D, где D ограничена линиями x=0, y=0, x+y=1
amur466676:
Двойной интеграл iint D (2y-3x) dxdy, где D - прямоугольник, ограниченный осями координат и прямыми x = 6 y = 1 равен:
Двойной интеграл iint D (2y-3x) dxdy, где D - прямоугольник, ограниченный осями координат и прямыми x = 6 y = 1 равен:
Ответ:
Ответ:
Ответы
Автор ответа:
0
Ответ:
Приложения:
Привет, помогите пожалуйста с заданием с математики в профиле внизу.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: аовтса
Предмет: Английский язык,
автор: buravlev95
Предмет: Математика,
автор: БупБупБуп