Предмет: Алгебра,
автор: nglushcov
помогите пожалуйста, нужно срочно!
Приложения:
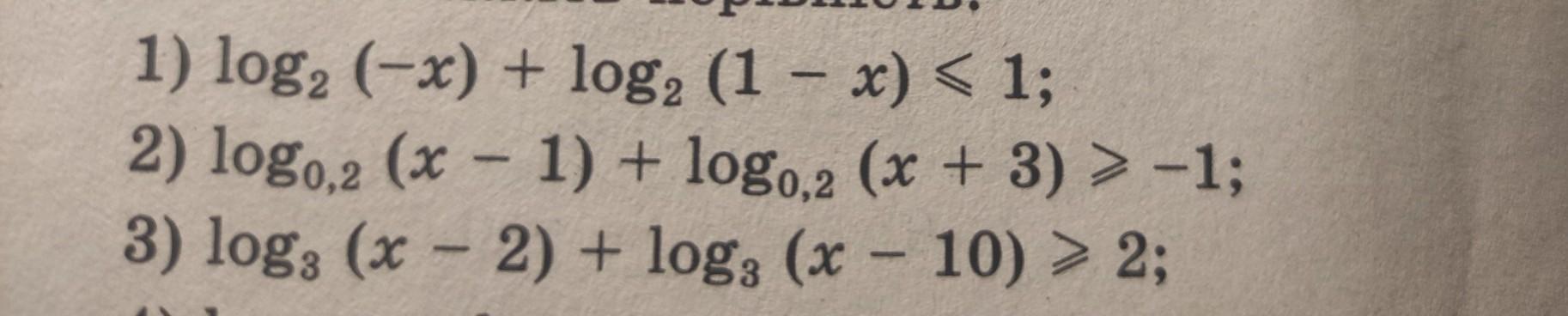
Ответы
Автор ответа:
1
Объяснение:
функция монотонно возрастает на всей D(y), поэтому возможна равносильная замена:
;
Графиком у=х²-х-2 будет парабола, ветви вверх, поэтому отрицательные значения будет принимать в промежутке между корнями х=-1 и х=2
no T. Buema:
[/tex] {x}^{2} + 2x - 8 = ({x}+ 4)(x - 2)\\ \begin{cases} ({x}+ 4)(x - 2) \leqslant 0 \\ x > 1 \end{cases}[/tex]
Графиком функции
y= x² + 2x - 8
будет парабола, ветви вверх, поэтому отрицательные значения будет принимать в промежутке между корнями х=-4и х=2
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: annakonopelcheva
Предмет: Русский язык,
автор: ололош5647т
Предмет: Математика,
автор: lazka20088446
Предмет: Алгебра,
автор: Aslanqa