Question

На фото. Можна без детального пояснення.​

Answer 1

Ответ:

Задача некорректно составлена, цилиндра с такими значениями не существует.

60см²

Объяснение:

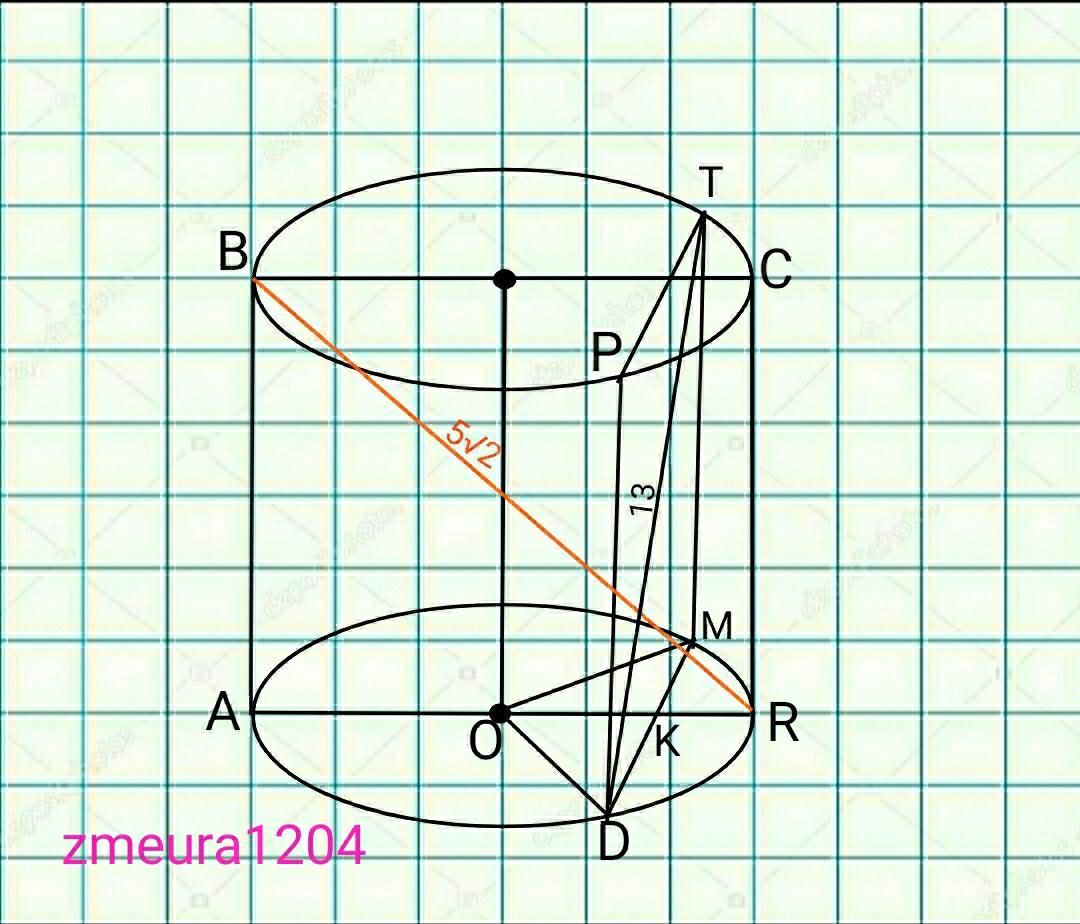
ABCR- квадрат.

BR=5√2см диагональ квадрата.

АВ=АR=BR/√2=5√2/√2=5см.

АВ=5см высота цилиндра.

АR=D=5см диаметр цилиндра.

Рассмотрим плоскость сечения DPTM.

TM=AB=5см.

ТD=13см, по условию

∆DTM- прямоугольный треугольник

По теореме Пифагора

DM=√(TD²-TM²)=√(13²-5²)=√(169-25)=

=√144=12см.

S(DPTM)=DM*MT=12*5=60см²

Ответ: площадь сечения 60см²

______________

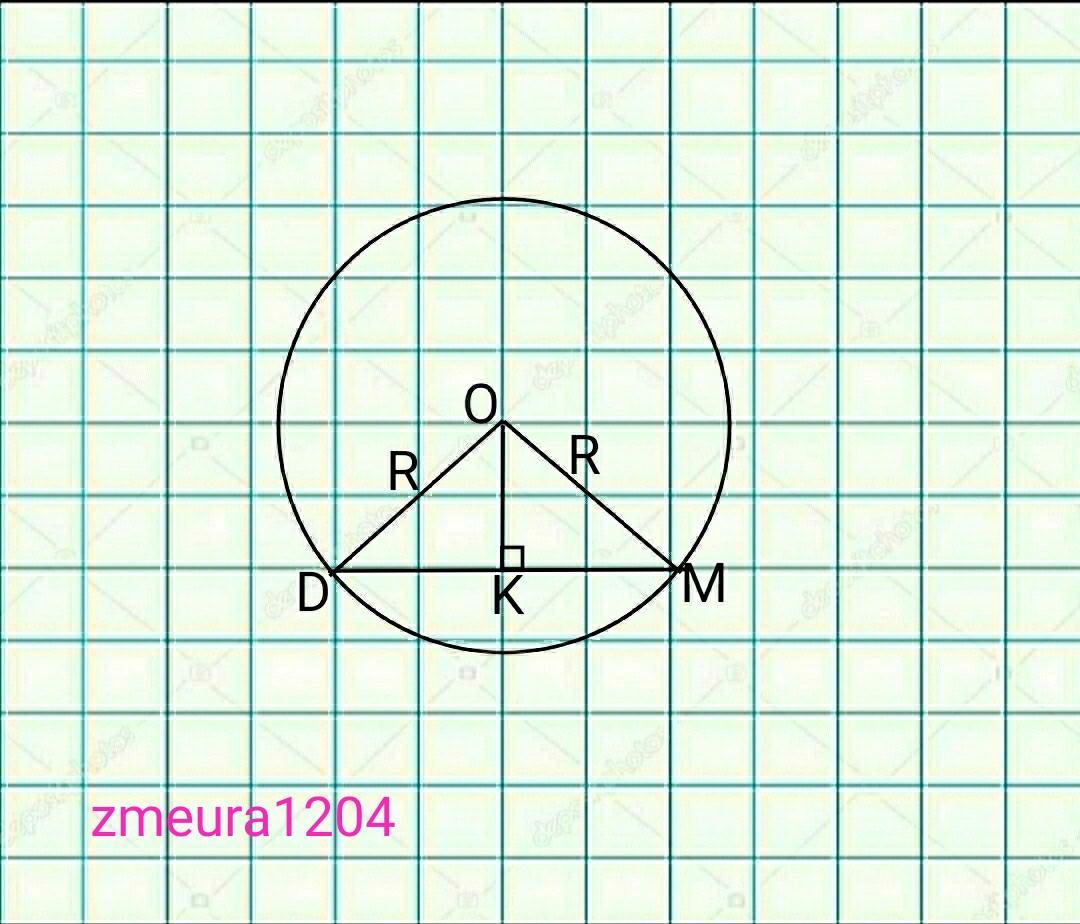
Найдем расстояние от центра окружности цилиндра до плоскости сечения.

∆DOM- равнобедренный треугольник

DO=OM=D/2=5/2=2,5см.

DM=12см

DK=KM=DM/2=12/2=6см

∆ОКМ- прямоугольный треугольник

КМ=6см катет

ОМ=2,5см гипотенуза.

Хорда DM не может быть больше диаметра АR.