Предмет: Алгебра,
автор: Аноним
Найти общее решение дифференциального уравнения.
Приложения:
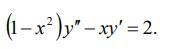
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Окружающий мир,
автор: хлебушек123456ук
Предмет: Английский язык,
автор: Makskoldj
Предмет: Окружающий мир,
автор: виктория710
Предмет: Математика,
автор: drak227
Предмет: Английский язык,
автор: sofia210104