Question

ПОМОГИТЕ ПОЖАЛУЙСТА С ОБЬЯСНЕНИЕМ

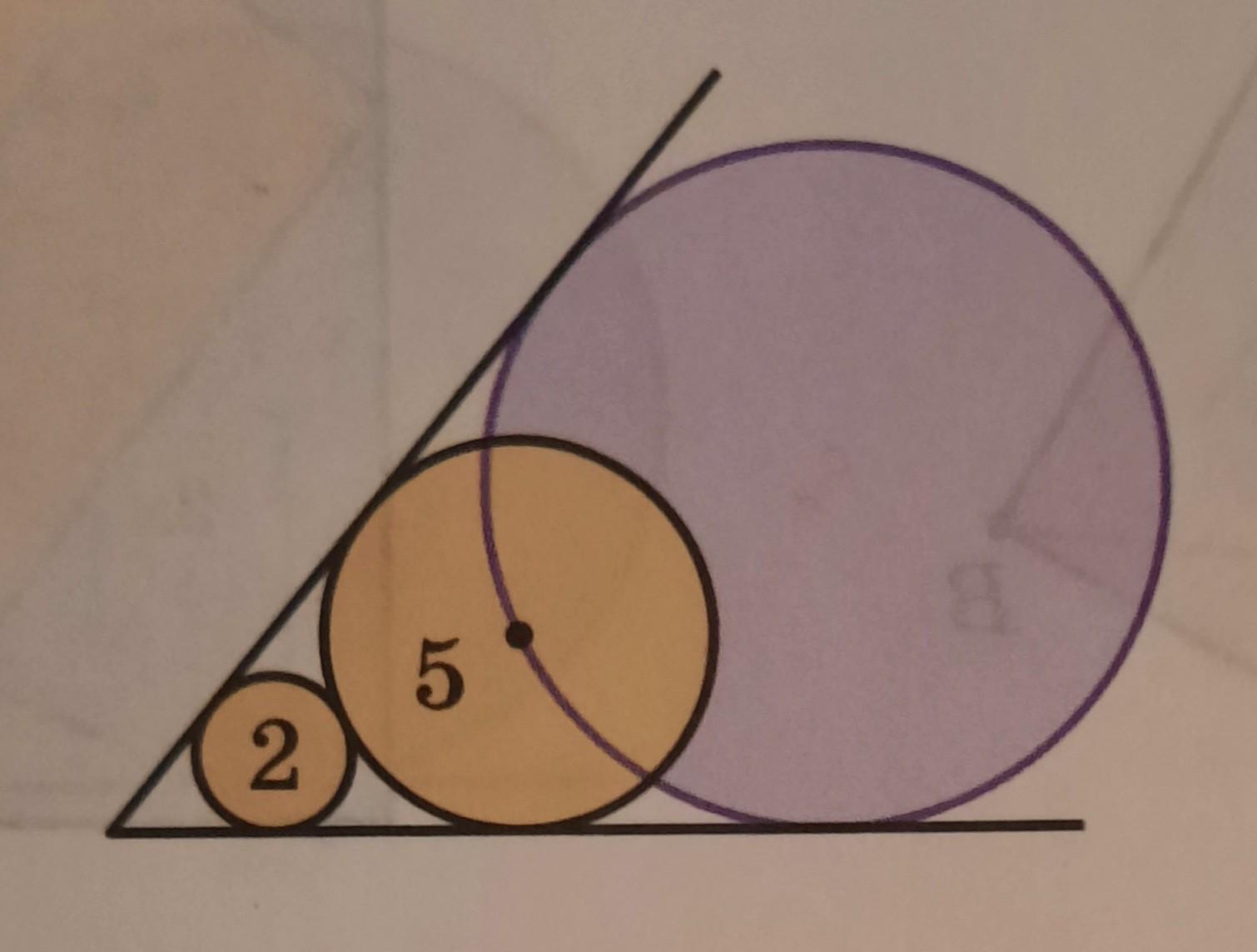
Две окружности с радиусами 2 и 5 вписаны в угол и касаются друг друга. Найдите радиус третьей окружности, вписанной в тот же угол и проходящей через центр большей из них.​

Answer 1

Две окружности с радиусами 2 и 5 вписаны в угол и касаются друг друга. Найдите радиус третьей окружности, вписанной в тот же угол и проходящей через центр большей из них.​

Объяснение:

Пусть О-центр третьей окружности, а х-ее радиус . Проведем луч ЕО.

1) По свойству радиуса , проведенного в точку касания , радиусы ОА ,НВ,РС будут перпендикулярны ЕА

2) Проведем НМ⊥ОА ⇒ НМ║ЕА, как 2-е прямые перпендикулярные третьей . Тогда  ∠МНО=∠АЕО как соответственные при НМ║ЕА, ЕО-секущая.

Проведем РК⊥НВ ⇒ РК║ЕА, как 2-е прямые перпендикулярные третьей . Тогда  ∠КРН=∠АЕО как соответственные при РК║ЕА, ЕО-секущая.

Значит ∠МНО=∠АЕО=∠КРН

3) ΔМНО~ΔКРН по двум углам : ∠М=∠К=90°, ∠МНО=∠КРН см.п2 ⇒ сходственные стороны пропорциональны : НО:РН=МО:КН .

Ищем длины отрезков

НО-это радиус , НО=х ; РН=2+5=7   ; МО=АО-АМ=х-5 ; КН=ВН-ВК=5-2=3.

$\displaystyle \frac{x}{7} =\frac{x-5}{3}$  , 7(х-5)=3х , 4х=35 , х=8,75 ед

Радиус третьей окружности 8,75 ед.