На границе Криптоландии установлена пропускная система, имеющая 20 входов и 20 выходов (входы перед границей, выходы – уже в Криптоландии). Входы и выходы занумерованы независимо друг от друга числами от 1 до 20, причем в неизвестном для посетителей Криптоландии порядке. От каждого входа проложен один «прямой» туннель к одному из выходов, причем от разных входов – к разным выходам. От каждого выхода проложен один «обратный» туннель ко входу с тем же номером, что у этого выхода. Посетитель сам выбирает один из входов. Войдя в него, он попадает в лифт, в котором есть 2 кнопки: зеленая – «ехать», красная – «выходить». Система работает следующим образом. Посетитель, находясь в лифте около входа, нажимает зеленую кнопку, лифт по прямому туннелю доставляет его к соответствующему выходу. Находясь в лифте около выхода, посетитель может: 1) нажать зеленую кнопку, и тогда лифт по обратному туннелю доставит его ко входу с тем же номером; 2) нажать красную кнопку, и тогда выход откроется, но только если его номер совпадает с номером того входа, через который посетитель вошел первоначально. В противном случае (при несовпадении номеров) посетитель будет удалён за пределы Криптоландии и сможет воспользоваться правом посещения только через год. Алиса решила провести каникулы в Криптоландии. При этом ей стала известна схема прямых туннелей системы пропуска:
Здесь верхнее число является номером входа, а стоящее под ним число – номером того выхода, к которому ведет прямой туннель. За какое минимальное число поездок по туннелям Алиса сможет гарантированно попасть в Криптоландию?
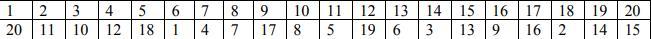
Ответы
Ответ:
За 5 поездок.
Объяснение:
Как я понял, процедура такая.
1) Алиса садится в лифт в любом входе x1.
2) приезжает на выход x2, потом едет обратно на вход x2.
3) снова едет, приезжает на выход x3, потом обратно на вход x3.
...
n) от входа xn снова едет, приезжает на выход x1. Здесь она может выйти.
Я составил таблицу путешествий, получилось вот что:
1 - 20 - 15 - 13 - 6 - 1. 9 поездок.
9, а не 5, потому что после 20 выхода надо ещё проехать на 20 вход.
И также на всех остальных выходах и входах.
2 - 11 - 5 - 18 - 2. 7 поездок.
3 - 10 - 8 - 7 - 4 - 12 - 19 - 14 - 3. 15 поездок.
4 - 12 - 19 - 14 - 3 - 10 - 8 - 7 - 4. 15 поездок.
5 - 18 - 2 - 11 - 5. 7 поездок.
6 - 1 - 20 - 15 - 13 - 6. 9 поездок.
7 - 4 - 12 - 19 - 14 - 3 - 10 - 8 - 7. 15 поездок.
8 - 7 - 4 - 12 - 19 - 14 - 3 - 10 - 8. 15 поездок.
9 - 17 - 16 - 9. 5 поездок.
Дальше я писать не буду, и так уже все ясно.
Минимальный путь начинается с 9, 16 или 17 входа и содержит 5 поездок.