Предмет: Алгебра,
автор: Аноним
Найти общее решение дифференциального уравнения.
Приложения:
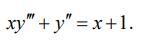
Ответы
Автор ответа:
2
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Fuhxfjcyjj0580158
Предмет: Английский язык,
автор: даша1613
Предмет: Русский язык,
автор: mardonbek
Предмет: Русский язык,
автор: nata6639
Предмет: Русский язык,
автор: fsdi