Question

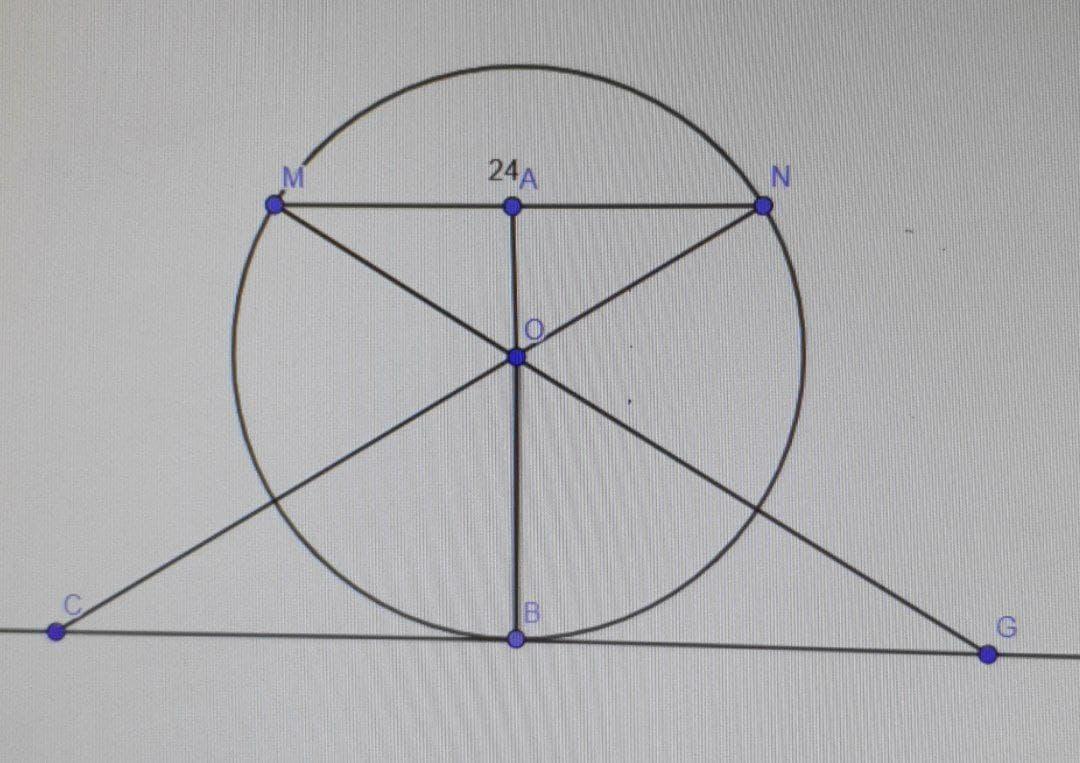
ПОЖАЛУЙСТА СРОЧНО НУЖНО НАДО.Радиус окружности с центром в точке О равени37 ,длина хорды MN равна 24.Найдите растояние от хорды MNдо параллелной её касательной b​

Answer 1

Ответ:

72

Объяснение:

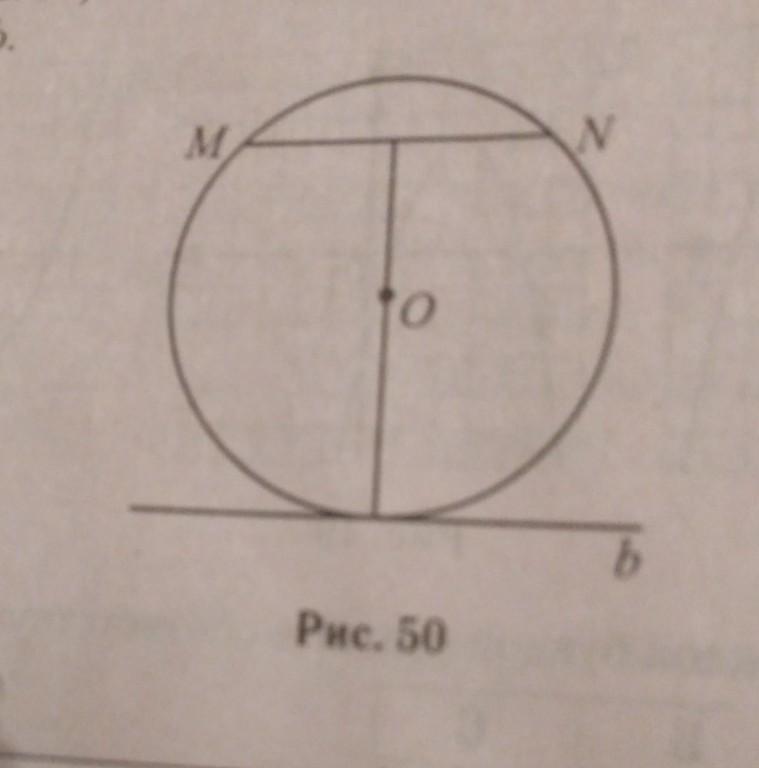
Дано: Окр. О,R.

MN = 24 - хорда; R = 37;

MN || b.

Найти: КТ.

Решение.

1. MN || b (условие)

• Радиус, проведённый в точку касания, перпендикулярен касательной.

⇒ КТ ⊥ b

• Если отрезок перпендикулярен одной из параллельных прямых, то он перпендикулярен и к другой прямой.

⇒ КТ ⊥ MN.

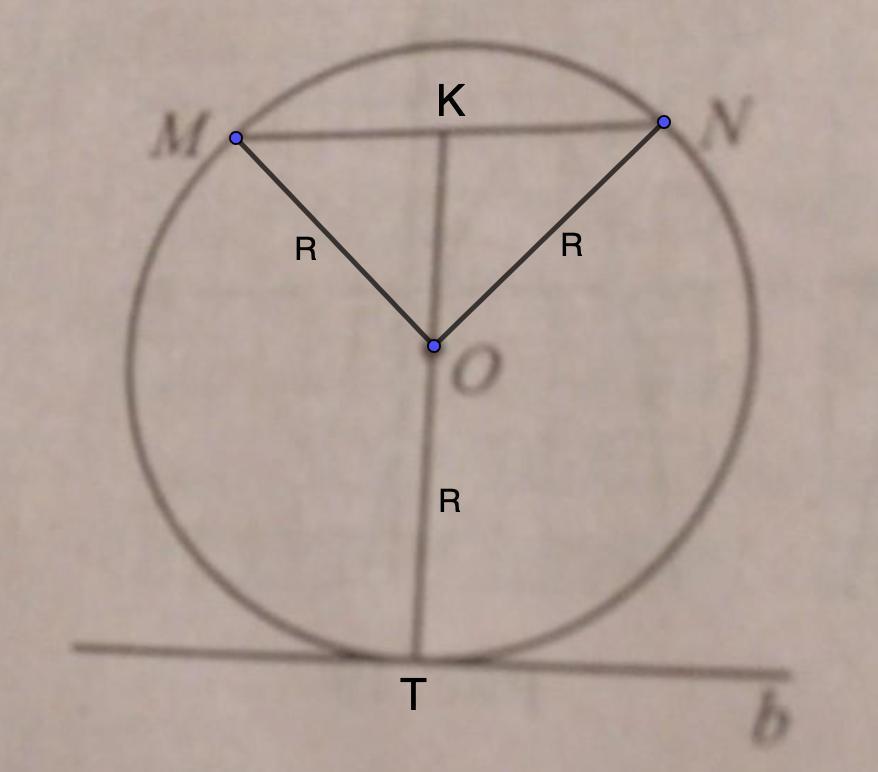
2. Рассмотрим ΔOMN.

OM = ON = R

⇒ ΔOMN - равнобедренный.

ОК - высота (п.1)

• В равнобедренном треугольнике высота , проведенная к основанию,  является медианой.

⇒ МК = KN = 24 :2 = 12

3. Рассмотрим ΔМКО - прямоугольный.

По теореме Пифагора:

ОК² = ОМ² - МК² = 1369 - 144 = 35

4. КТ = ОК + ОТ = 35 + 37 = 72

Answer 2

Ответ:

72

Объяснение:

Дано: R=ОВ=37, MN=24 MN║b (MN║CG)

Найти: АВ

Т.к.  CG - касательная к окружности, то по свойству касательных:

ОВ⊥ CG (Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.) ∠GBO = 90°

∠МАО=∠GBO = 90° (внутренние накрест лежащие углы при параллельных прямых MN и CG и секущей АВ)

ΔМАО=ΔNAO - по гипотенузе и катету ( катет АО - общий, МО=ON - как радиусы) ⇒МА=АN=MN/2=24/2=12

ON = 37, как радиус окружности.

ΔAON (∠A=90°) : по теореме Пифагора АО²= ON²-АN²=37²-12²=1225

АО=√1225=35

АВ= АО+ОВ=35+37=72