Предмет: Алгебра,
автор: Аноним
Даю 100 баллов за решение!!!
Приложения:
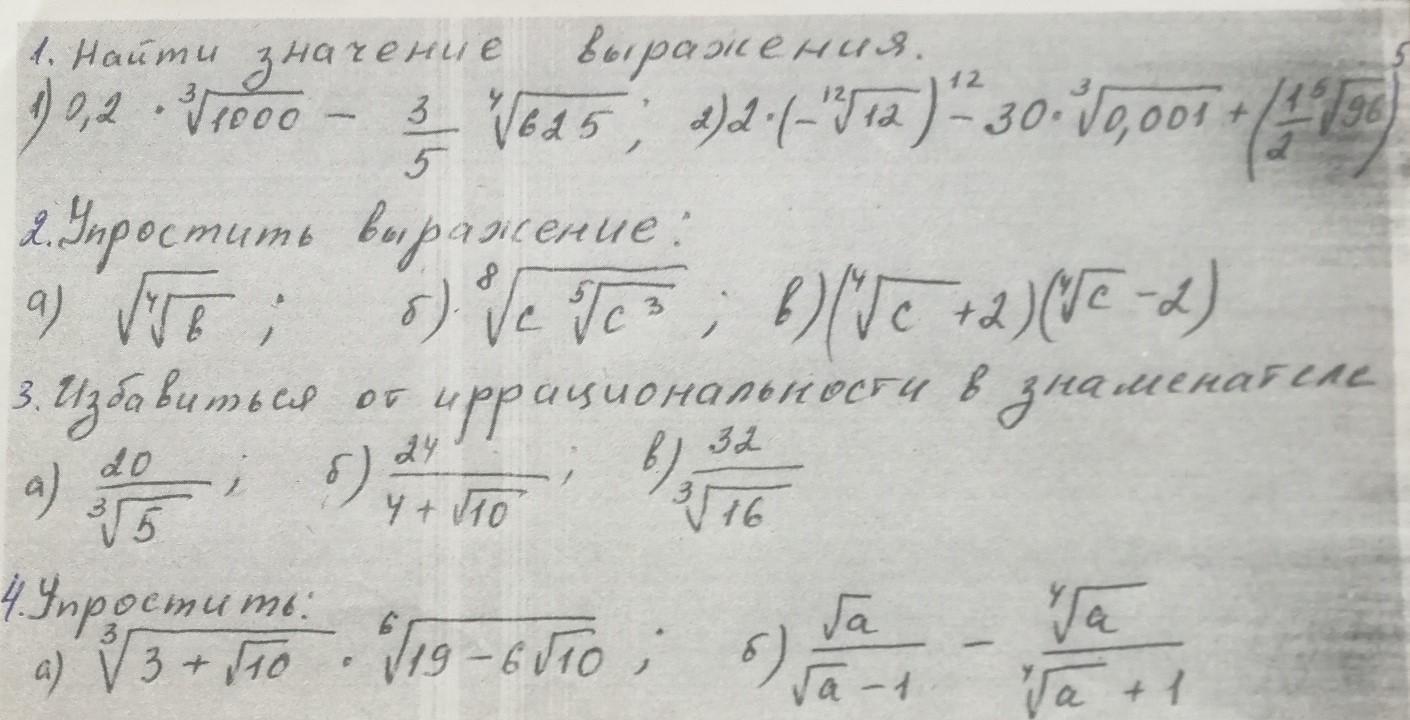
Ответы
Автор ответа:
1
Часть решения
Первое задание
Второе задание
Четвертое задание
(упростим)
Похожие вопросы
Предмет: Другие предметы,
автор: gloriamakfin2
Предмет: Русский язык,
автор: Artem11246
Предмет: Английский язык,
автор: полина579
Предмет: Математика,
автор: vera1901
Предмет: Русский язык,
автор: asiya224