Question

ПОМОГИТЕЕЕЕ
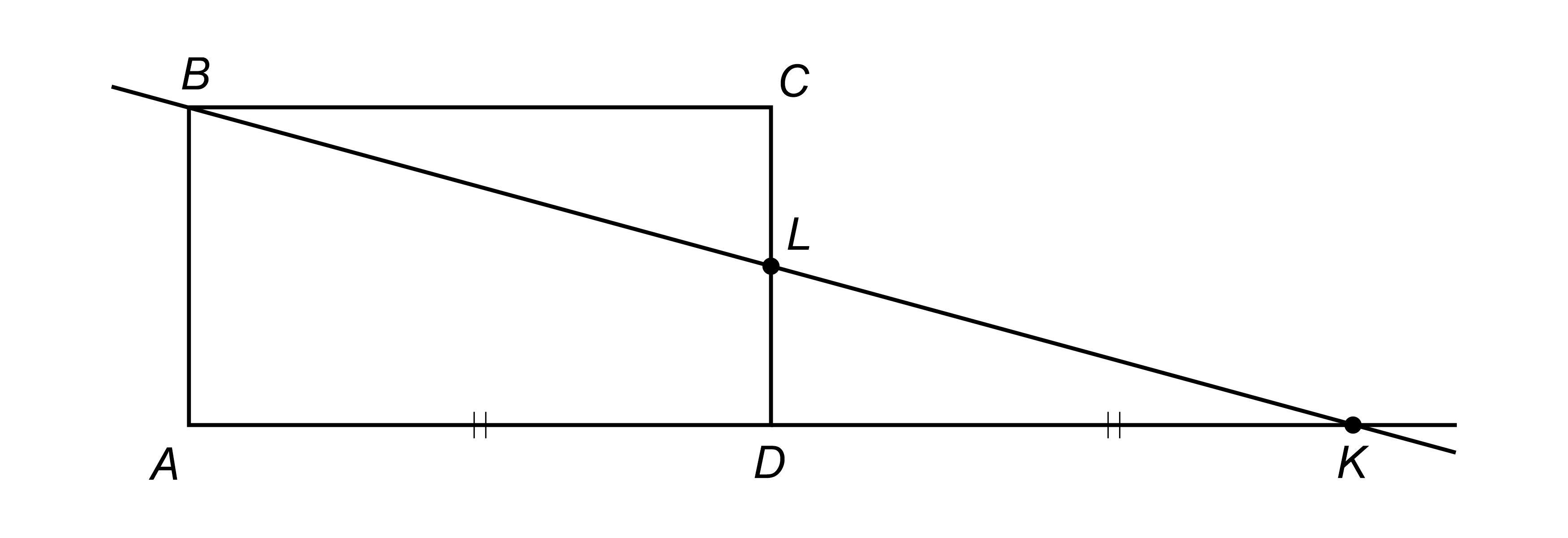
Через вершину В прямоугольника ABCD проведена прямая, пересекающая продолжение стороны AD в точке K так, что AD = DK. Периметр прямоугольника  равен 34 см, а сторона ВС на 5 см  больше АВ. Найдите площадь треугольника АВK.
​

Answer 1

Ответ:

S (Δ АВK) = 16,5 cm²

Объяснение:

Т.к. AD = DK, ⇒ BK делит CD по полам, тоесть CL = LD = CD/2

Обозначим AB = x, ⇒ BC = x + 5

Периметр прямоугольника = 2 × (AB + BC)

Подставляем значения, и находим чему равен x:

2 × (x + x + 5) = 34

2x + 2x + 10 = 34

4x = 34 - 10

4x = 24

x = 24/4

x = 6 см = AB = CD

⇒ BC = AD = x + 5 = 6 + 5 = 11 см

Рассмотрим Δ АВK - это прямоугольный Δ

Площадь прямоугольного треугольника равна:

S (Δ АВK) = (LD × DK)/2

LD = CD/2 = 6/2 = 3 см, DK = AD = 11 cm

Подставляем значения:

S = (3 × 11)/2

S = 33/2

S = 16,5 cm²