Предмет: Математика,
автор: threekitka15
Помогите пожалуйста даю 20 баллов
Приложения:
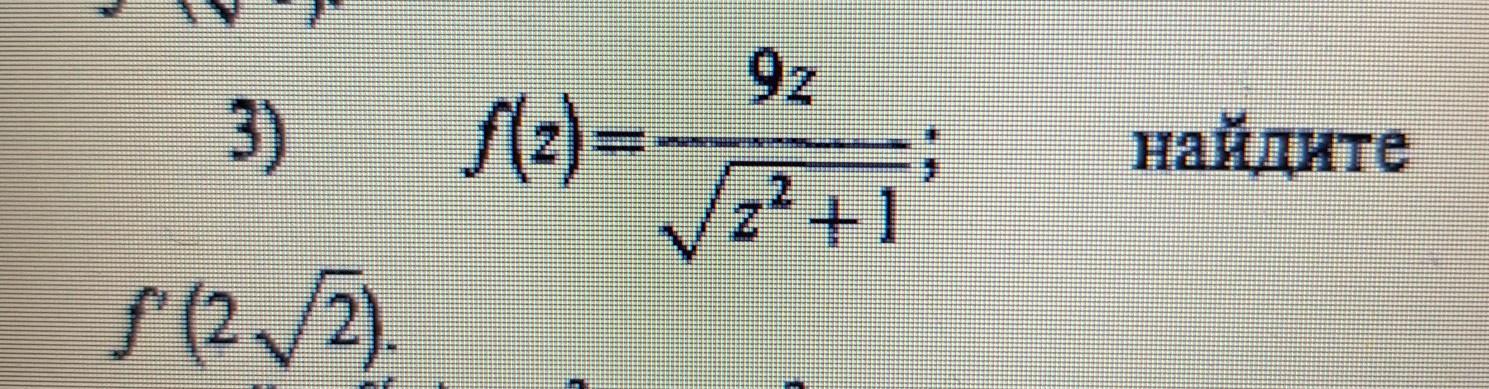
Ответы
Автор ответа:
0
Надеюсь все понятно……
Приложения:
Автор ответа:
0
Ответ:
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: 2006182
Предмет: Русский язык,
автор: РозаАлексеева
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Алгебра,
автор: nicolay46
Предмет: Русский язык,
автор: lol1951