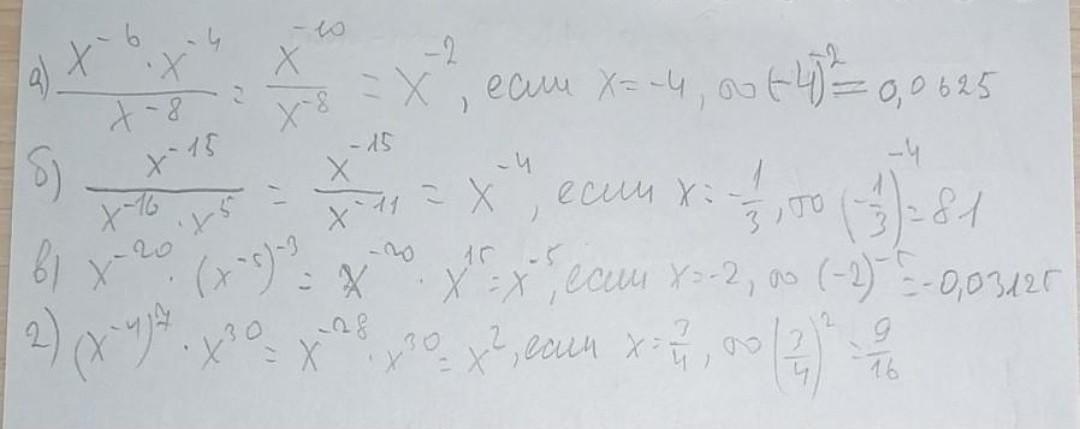Помогите прошу
Все подробно расписано должно
нифига не понимаю, помогите пожалуйста!!
Тема: применение свойств степени с целым показателем
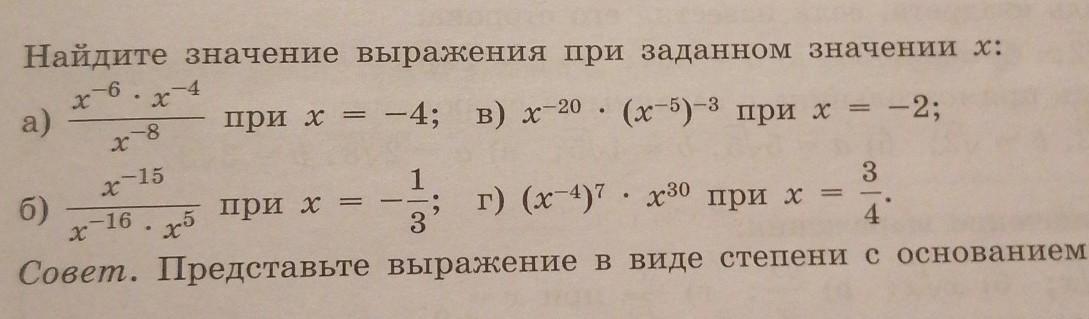
Ответы
Внизу есть Совет : "представьте выражение в виде степени с основанием х".
Те, если у выражения есть подобные основания(в данном случае х), то можно выполнять действия со степенями. Дальше нужно просто запомнить
1) при умножении степени с одинаковыми основаниями показатели складываются. Что я и сделал под буквой а в числителе. х^(-6+(-4)=х^(-10). Это объяснить просто. Понятно же что х*х это х², тут мы сложили значения степеней(х¹*х¹=х^(1+1)). Или же перемножили х два раза. Нужно понимать что х³ можно представить как х*х*х, а х⁴ как х*х*х*х. Если перемнижить х³*х⁴, это тоже самое, что и х*х*х*х*х*х*х. Семь раз перемножили х.
2)при делении степеней с одинаковыми основаниями из показателя делимого вычитают показатель делителя. Принцип такой же что и при умножении. х⁴/х³ - числитель можем представить как х*х*х*х, а знаменатель х*х*х. Соответственно х*х*х*х/х*х*х, сократить все иксы и останется х.(х^(4-3)=х¹).
3)при возведении степени в степень показатели перемножаются. (х³)², тоже самое что х³*х³, а тут уже по принципу умножения степени с одинаковыми основаниями, и получится х^6
Нужно прорешать несколько таких примеров, чтобы закрепить это понятие, и совсем скоро это дойдёт до уровня автоматизма, такие примеры не булут для тебя сложными. Надеюсь объяснил понятно:)