Предмет: Алгебра,
автор: epicgameesmm
решите пример,и объясните решение,подробно пжжж
Приложения:
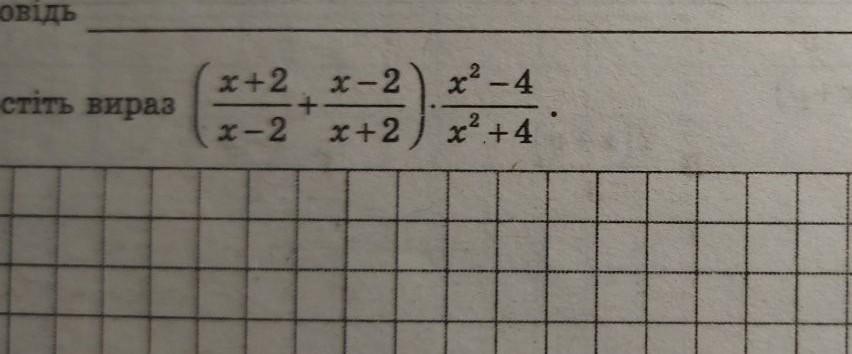
Ответы
Автор ответа:
1
Ответ:
2
Объяснение:
1) записываем все числители над наименьшим общим знаменателем (х-2)(х+2)
2)используя а²-b² = (a-b)(a+b), разложить множители выражение
3)сокращаем на х-2 и на х+2
4)вычисяляем произведение
5)используя (а+в)² = а²+2ав+в² и (а-в)² = а²-2ав-в² записать всё в развёрнутом виде
6)сумма двух противоположенных величин равно 0 так что убираем +4х и -4х, а остально всё складываем
7) выносим за скобку множитель (2)
сокращаем дробь
РЕШЕНИЕ В ВИДЕ ПРИМЕРА:
(х+2)²+(х-2)²/(х-2)(х+2)×(х-2)(х+2)/х²+4
((х+2)²+(х-2)²)×1/х²+4
(х+2)²+(х-2)²/х²+4
х²+4х+4+х²-4х+4/х²+4
2х²+8/х²+4
2(х²+4)/х²+4
ответ: 2
Автор ответа:
1
Ответ:
2
Объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: alinanya11
Предмет: Английский язык,
автор: geger2000
Предмет: Окружающий мир,
автор: милана315
Предмет: Українська мова,
автор: vikusaavzabarova
Предмет: Русский язык,
автор: Пσԉüнα