Предмет: Алгебра, автор: LakiMaki

100 бал. срооочно!!!!!

Приложения:

Ответы

Автор ответа: MizoriesKun

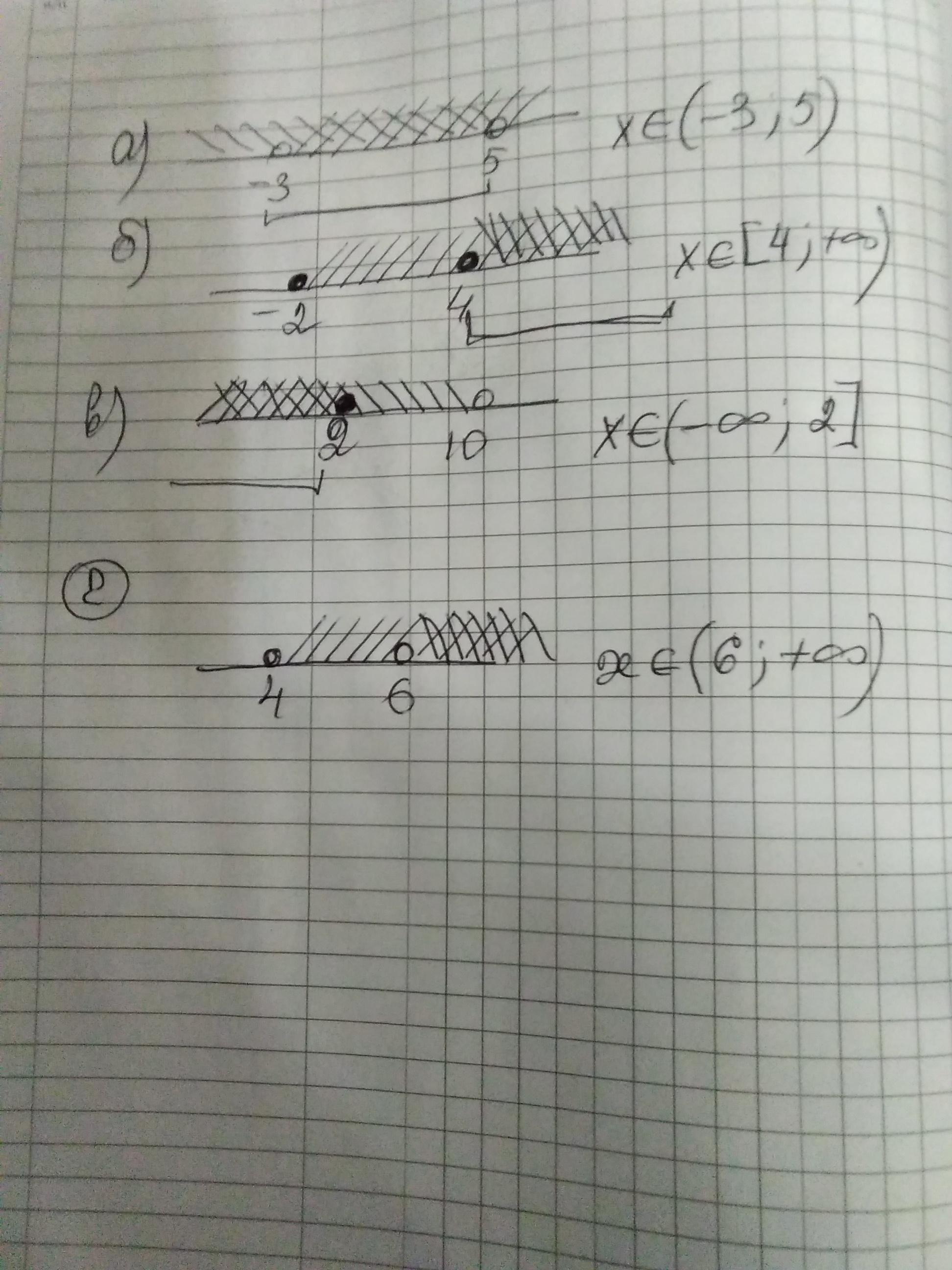
а) х∈ (-3;5)

б) х∈ [4: +∞)

в) х∈ (-∞; 2]

$\left \{ {{6x-24>0} \atop {-2x+12<0}} \right.$

$\left \{ {{6x>24} \atop {-2x<-12}} \right.$

$\left \{ {{x>4} \atop {x>6}} \right.$

x∈ (6; +∞)

Приложения:

LakiMaki: спасибо

kamilmatematik100504: (в б) разве нет дополнительного решения {-2} ? Там же стоит знак больше либо равно) ?

LakiMaki: нет нету

LakiMaki: я сама всё прорешала ещё раз

LakiMaki: у меня как у старшего модератора

LakiMaki: получилось

LakiMaki: может я конечно не права

MizoriesKun: нет никаких доп. решений , ибо минус два не удовлетворяет второму неравенству

MizoriesKun: а решение системы ,это все значения удовлетворяющие обоим неравенствам одновременно

kamilmatematik100504: да хотя но если разобраться то при умножении мнимого числа на ноль выходит ноль ;
и тогда если у нас неравенство (x+2)√(x-4) ≥0 то выйдет что
при x =-2 ; то выйдет (2-2)√(-6)=0*√(-6)=0 как видите равенство выполняется но тут присутствует немного высшей математики так что поэтому это решение ; и не рассматривают

Автор ответа: kamilmatematik100504

Ответ:

Объяснение:

№1

$a) \displaystyle \begin{cases} x>-3 \\\\ x<5\end{cases} \Leftrightarrow x \in (-3 \ ; \ 5 ) \\\\\\\\ b) \displaystyle \begin{cases} x\geq -2 \\\\ x\geq 4\end{cases} \Leftrightarrow \begin{cases} x=-2 \\\\ x\geq 4 \end{cases} \Leftrightarrow x \in [4 \ ; \ \infty )$

№2

$\displaystyle \begin{cases} 6x-24>0 \\\\ -2x+12<0 \end{cases} \Leftrightarrow \begin{cases} 6x>24 \\\\ -2x<-12 \end{cases} \Leftrightarrow \begin{cases} x>4 \\\\ x>6 \end{cases} \ \Leftrightarrow \ x> 6 \ \ \Leftrightarrow \ \ x\in (6 \ ; \ \infty )$