Предмет: Геометрия,
автор: febuk2
Основание треугольника ровно 1 найдите длину отрезка, который соединяет середины двух его медиан, проведенных к боковым сторонам треугольника. СРОЧНО 50 БАЛОВ
Ответы
Автор ответа:
16
Ответ:
0,25
Объяснение:
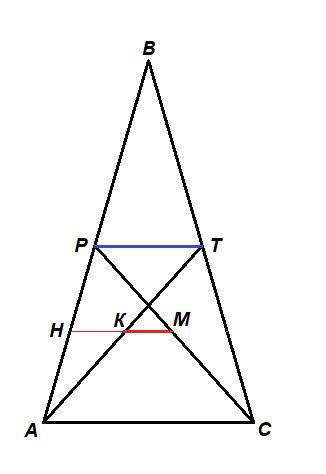
АТ и СР - медианы, проведенные к боковым сторонам равнобедренного треугольника АВС.
РТ - средняя линия треугольника АВС, значит
РТ = 1/2 АС = 1/2 · 1 = 0,5
Пусть М - середина СР. Проведем МН║АС (Н ∈ АВ), тогда по теореме Фалеса Н - середина АР.
МН - средняя линия треугольника АРС, значит
МН = 1/2 АС = 0,5
МН пересекает АТ в точке К.
Н - середина АР, НК║АС, а значит и НК║РТ, ⇒ по теореме Фалеса К - середина АТ.
НК - средняя линия треугольника АРТ.
НК = 1/2 РТ = 1/2 · 0,5 = 0,25
КМ - искомый отрезок.
КМ = МН - НК = 0,5 - 0,25 = 0,25
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Сто10000
Предмет: Русский язык,
автор: Алинка0931
Предмет: Русский язык,
автор: даданет
Предмет: Математика,
автор: XxOLGAxX
Предмет: Математика,
автор: aiym2007kasimova