Предмет: Алгебра,
автор: Аноним
Найти общее решение или общий интеграл дифференциального уравнения. Решить задачу Коши.
Приложения:
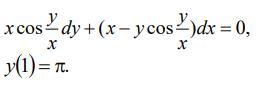
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: Настасья2108
Предмет: Українська література,
автор: linchiks1
Предмет: Другие предметы,
автор: tatyanami
Предмет: Математика,
автор: cheergun
Предмет: Русский язык,
автор: dipatov2000