Question

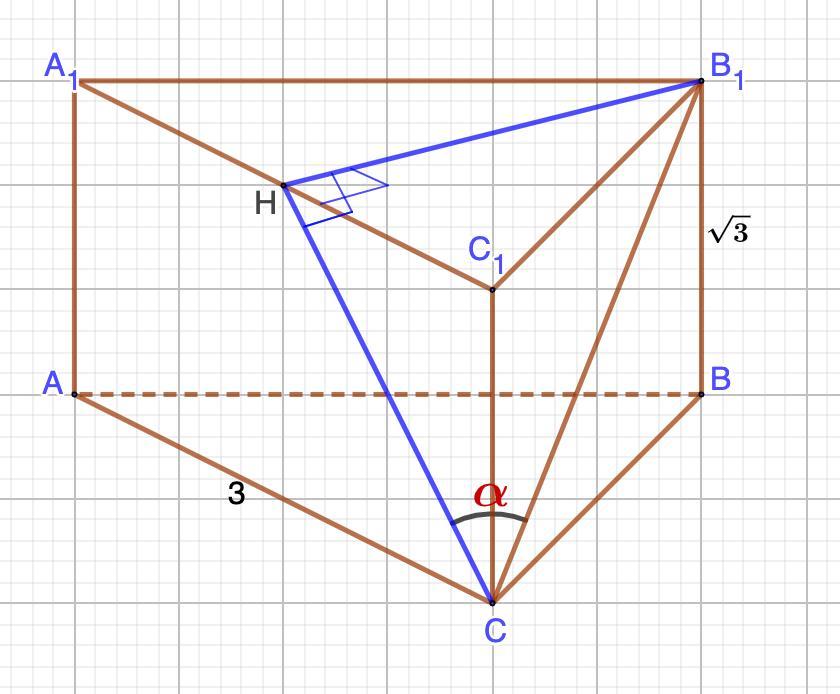
В правильной треугольной призме АВСА1В1С1 ребро основания равно 3, а боковое ребро равно корень из 3. Найдите синус угла между прямой В1С и плоскостью АСС1.
Пожалуйста, с рисунком.

Answer 1

Ответ:

sinα = 3/4

Объяснение:

Дано: АВСА₁В₁С₁ - правильная призма.

АС = 3; ВВ = √3.

Найти: sinα

Решение:

• Угол между прямой и плоскостью - угол между прямой и ее проекцией на это плоскость.

⇒ В₁Н ⊥ АСС₁

1. Рассмотрим ΔСВ₁В - прямоугольный.

По теореме Пифагора:

$CB_1=\sqrt{CB^2+BB_1^2} =\sqrt{9+3}=2\sqrt{3}$

2. Рассмотрим ΔНВ₁С₁  - прямоугольный.

• В равностороннем треугольнике высота является медианой.

⇒ $\displaystyle A_1H=HC_1=\frac{3}{2}$

По теореме Пифагора:

$\displaystyle B_1H=\sqrt{B_1C_1^2-HC_1^2}=\sqrt{9-\frac{9}{4} } =\sqrt{\frac{27}{4} } =\frac{3\sqrt{3} }{2}$

3. Рассмотрим ΔВ₁НС - прямоугольный.

• Синус угла - отношение противолежащего катета к гипотенузе.

⇒

$\displaystyle sin\alpha =\frac{HB_1}{CB_1}=\frac{3\sqrt{3} }{2*2\sqrt{3} } =\frac{3}{4}$