Предмет: Алгебра,
автор: Phedwassmin
Помогите решить неравенства логарифмов!
Приложения:
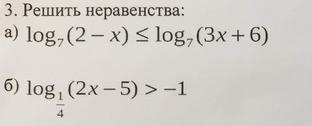
Ответы
Автор ответа:
4
Ответ:
Объяснение:
a)
б)
Похожие вопросы
Предмет: Русский язык,
автор: MASHAqeew
Предмет: Английский язык,
автор: волчица35
Предмет: Русский язык,
автор: некит588
Предмет: Литература,
автор: polina2555460