Даны четыре точки A, B, C . Составить уравнения: 1) плоскости ABC ; 2) прямой AB ;
3) найти расстояние от точки D до плоскости ABC .
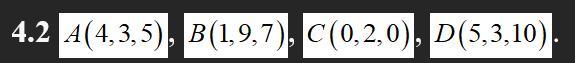
Ответы
Ответ:
Решение. A(0; 7; 1), B(2; -1; 5), C(1; 6; 3), D(3; -9; 8).
a) Уравнение плоскости, проходящей через три точки имеет вид:
- x1 y - y1 z - z1
X2 - x1 У2 - У1 Z2 - Z1 = 0. X3 - X1 Уз - У1 Z3 - Z1l
Чтобы составить уравнение плоскости АВС, одсталяем координаты точек A(0; 7; 1), B(2; -1; 5), C(1; 6; 3):
|x - 0 y-7 z - 1 2 - 0 -1 - 7 5 - 1 = 0, 1 - 0 6 - 7 3 - 1
y-7 z - 1 -8 4 -1 2
= 0,
-16x - 2(z - 1) + 4(y - 7) + 8(z - 1) + 4x - 4(y - 7) = 0, -16x - 2z + 2 + 4y - 28 + 8z - 8 + 4x - 4y + 28 = 0, -12x + 6z - 6 = 0, 2x - z + 1 = 0 - уравнение плоскости АВС.
б) Уравнение прямой, проходящей через две точки, имеет вид:
X2 - X1 У2 - У1 Z2 - Z1
Подставив координаты точек А(0; 7; 1) и В(2; -1; 5), получим: x - 0 у - 7 z - - 1 2 - 0 -1 -7 5-1
2
-8
- 1
4
уравнение прямой АВ.
b) Из уравнения плоскости АВС 2х - z + 1 = 0 определяем координаты нормального вектора плосксти: n(2; 0; -1). Нормальный вектор плоскости является направляющим вектором прямой DM, перпендикулярной к плоскости АВС. Уравнение прямой, проходящей через точку M(хo; Уо; Zo) и имеющей направляющий вектор q(l; m; n), имеет вид: