2 задачи по геометрии с объяснением того как вы это решили
Ответы
Відповідь:
Пояснення:
Чтобы определить угол между векторами необходимо соединить начало этих векторов.
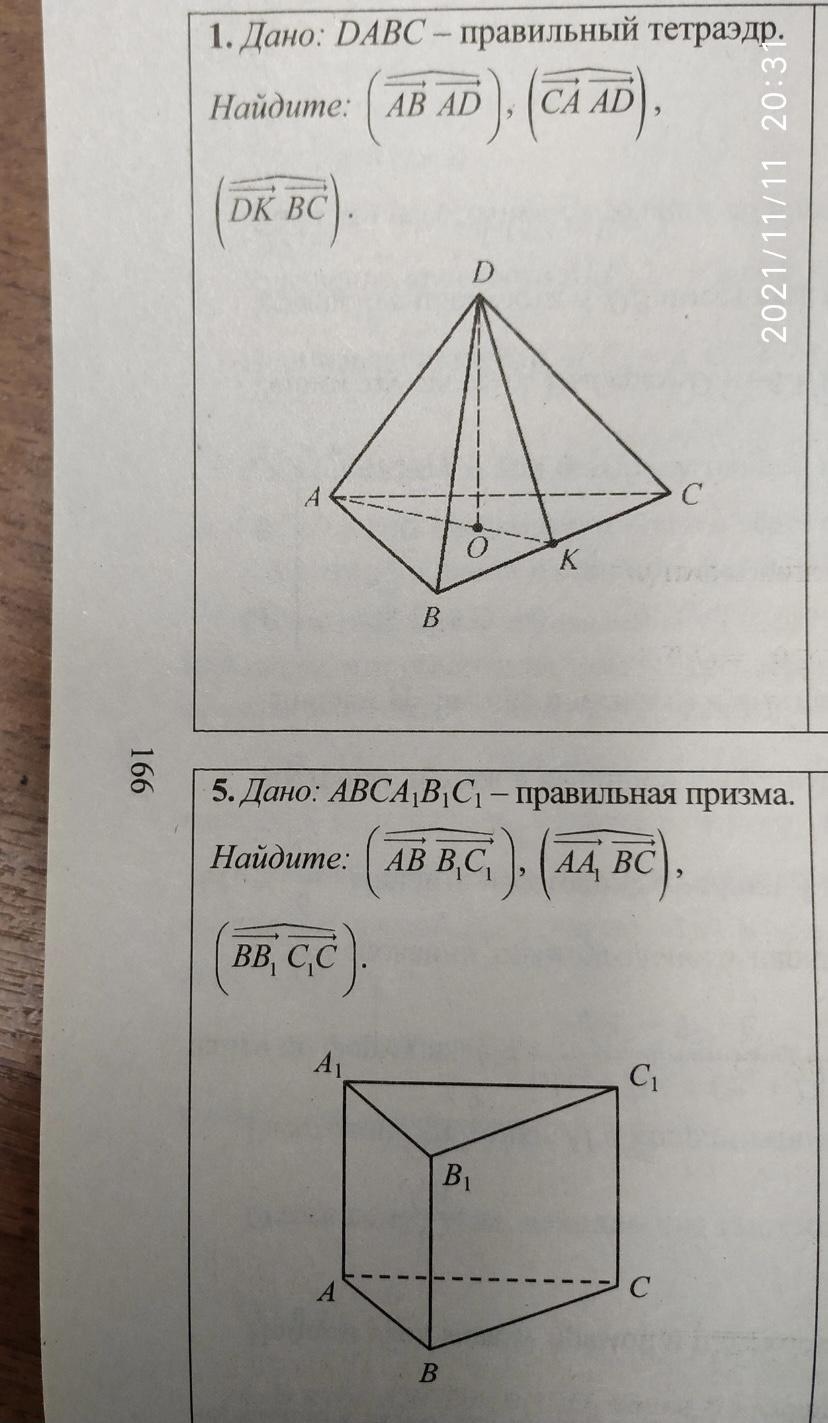
1. Так как DABC- правильный тетраэдр, то каждая грань есть равносторонние треугольники, с углами в 60°
Вектора АВ и AD находятся в одной плоскости и выходят с одной точки, поэтому
угол между этими векторами равен углу BAD=60°,
Угол (CA, AD)=120°,
Рассмотрим треугольник ADC. Параллельно перенесем вектор CA в вершину А, тогда угол между векторами CA, AD будет равен внешнему углу треугольника ADC при вершине А
Так как треугольник АBC - правильный, то АK - медиана, высота и биссектриса -> АК перпендикулярна ВС. DK- медиана и высота, так как BDC правильный треугольник. -> вектора ВС и DK перпендикулярные, то угол (DK, BC) =90°
2.
Треугольник АВС-правильный
Проекцией В1С1 на плоскость ВАС есть ВС. Продолжим прямую АВ, перенеся начало вектора АВ в вершину В. Тогда угол между АВ и В1С1 равен внешнему углу треугольника АВС и =120°
Так как АА1||ВВ1, то угол между векторами АА1 и ВС равен углу В1ВС=90°
ВВ1||С1С, но вектора противоположно направленные, поэтому угол между ними равен 180°