Question

Дана правильная треугольная пирамида высота которой равна 2 см, а апофема 4 см. Найдите площадь боковой поверхности

Answer 1

Ответ:

ответ на фото

Объяснение:

площадь боковой поверхности умножим на три 12*3= 72

Answer 2

Ответ:

72см²

Объяснение:

Дано:

МАВС- правильная треугольная пирамида

ABC- равносторонний треугольник.

МР=4см апофема.

МО=2см высота.

Sбок=?

_____

Решение

∆МРО- прямоугольный треугольник.

По теореме Пифагора

РО=√(МР²-МО²)=√(4²-2²)=√(16-4)=

=√12=2√3 см радиус вписанной окружности в основание пирамиды.

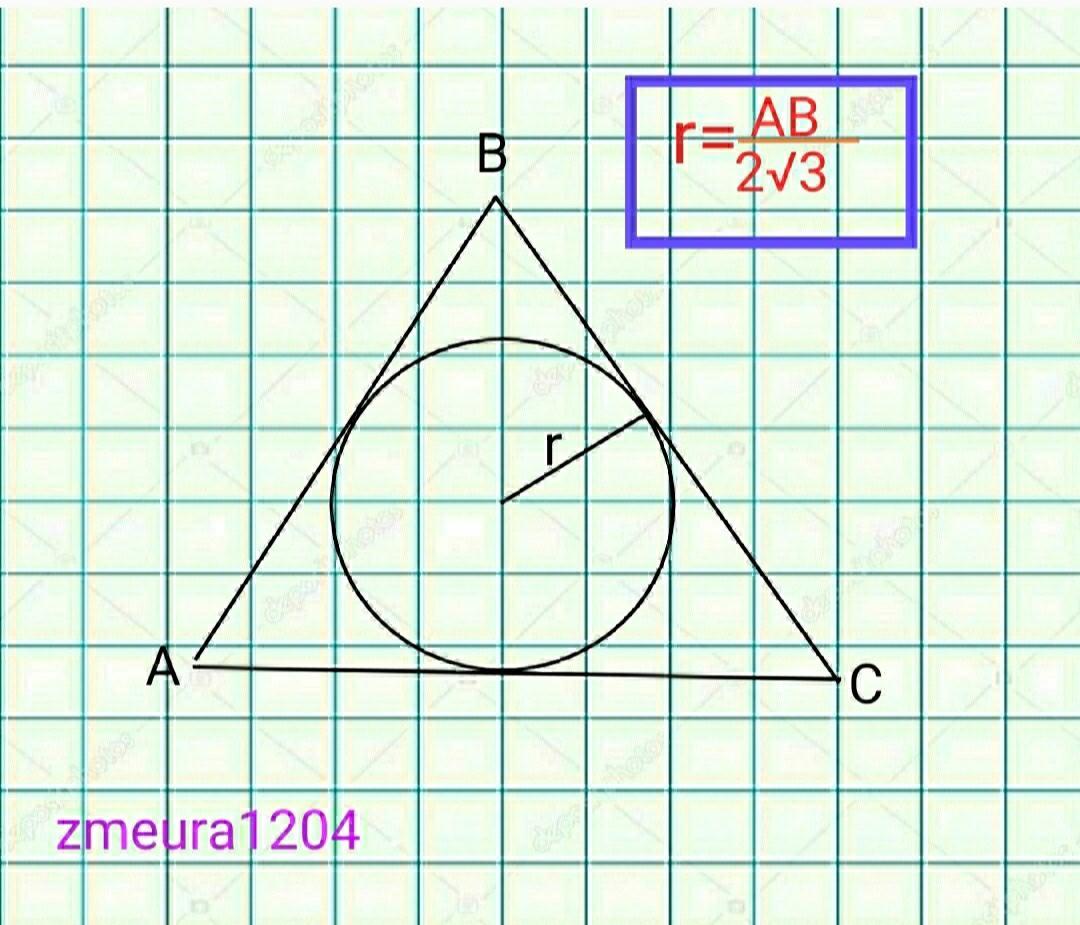
Из формулы радиуса вписанной окружности в равносторонний треугольник.

r=AB/2√3, где АВ- сторона треугольника.

АВ=r*2√3=2√3*2√3=4*3=12см.

Росн=3*АВ=3*12=36

Sбок=1/2*Росн*РМ=1/2*36*4=72см²