Предмет: Геометрия,
автор: dombazz111
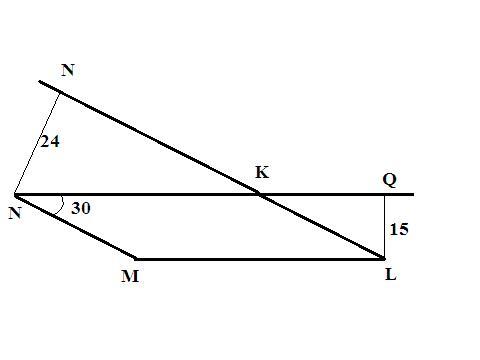
Дан параллелограмм MNKL , ∠NML=30° . Высота, проведенная из вершины NN к стороне LK, равна 24 . А высота LQ , проведенная к стороне NK равна 15 . Найди площадь параллелограмма.
Ответы
Автор ответа:
2
Ответ:
Объяснение:
∡К в параллелограмме - (180-30)=150°;
ΔKQL - прямоугольный, ∡К=(180-150)=30°,QL - катет против угла 30°, KL - гипотенуза - QL*2=15*2=30;
площадь - сторона умноженная на высоту проведенную к ней -
S=KL*NN=30*24=720 ед².
Приложения:
dombazz111:
уверен?
абсолютно
неправильно
я дурак
я две N написал
все равно спасибо
а что неправильно?
я две N написал видимо из за этого ты решил по другому
там еще 1 попытка
там как ни назови - принцип решения один и тот же.
Автор ответа:
1
Ответ:
720 ед²
Объяснение:
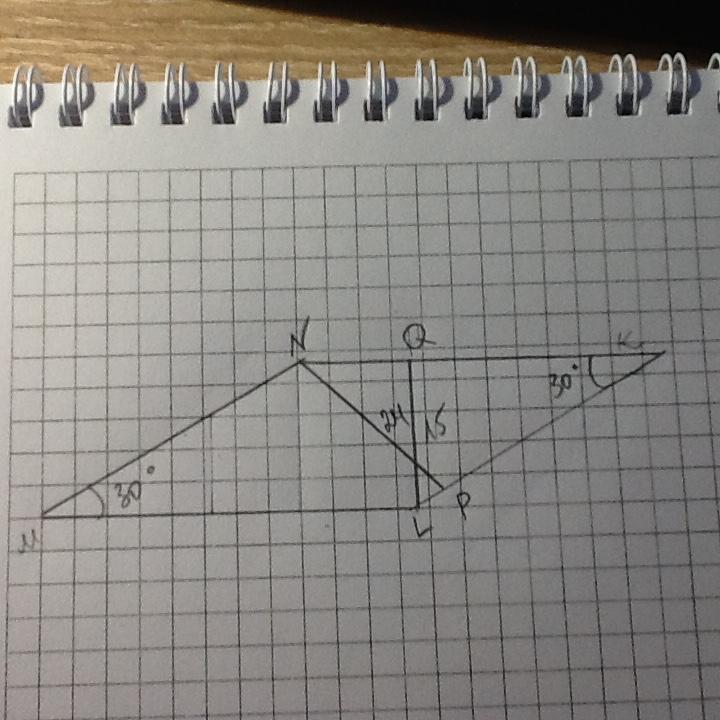
Дано: MNKL - параллелограмм, ∠NML=30°, NP=24, LQ=15. Найти S.
ΔKQL - прямоугольный, QL=1/2 KL по свойству катета, лежащего против угла 30°; KL=15*2=30.
S=KL*NP=30*24=720 ед²
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: никитка39
Предмет: Английский язык,
автор: Шоха000
Предмет: Русский язык,
автор: Мария11111111254
Предмет: Русский язык,
автор: economicfin2016
Предмет: Алгебра,
автор: MemeLom1919