Предмет: Алгебра,
автор: Novaya22
100 баллов! срочно! решить неравенство

Ответы
Автор ответа:
0
Ответ: (3; +Б)
Объяснение: (V- корень, ^ -знак степени)
V(3x+7) <x+1, надо решить систему { (1) 3x+7>=0,
(2) x+1>0, (3) 3x+7< (x+1)^2, решаем (1), x>=-7/3,
решаем (2), x> -1 , из (1) и (2) следует x>-1, решаем (3)
3x+7<x^2+2x+1, x^2-x-6>0, корни x=-2 u x=3, метод интервалов,
\\\\\\\\\\\\\+\\\\\\(-2)_____-______(3) \\\\\\\\+\\\\\\\\\ ,добавляем
решение x>-1 и ответ: x>3
Novaya22:
напишите на листе. вообще ничего не понятно из этой записи
Автор ответа:
1
ОДЗ:
Решением системы является
Возведём в квадрат обе части исходного неравенства:
Перекинем всё на одну сторону и разложим на множители:
Решение неравенства методом интервалов с учётом ОДЗ на фотографии
Приложения:
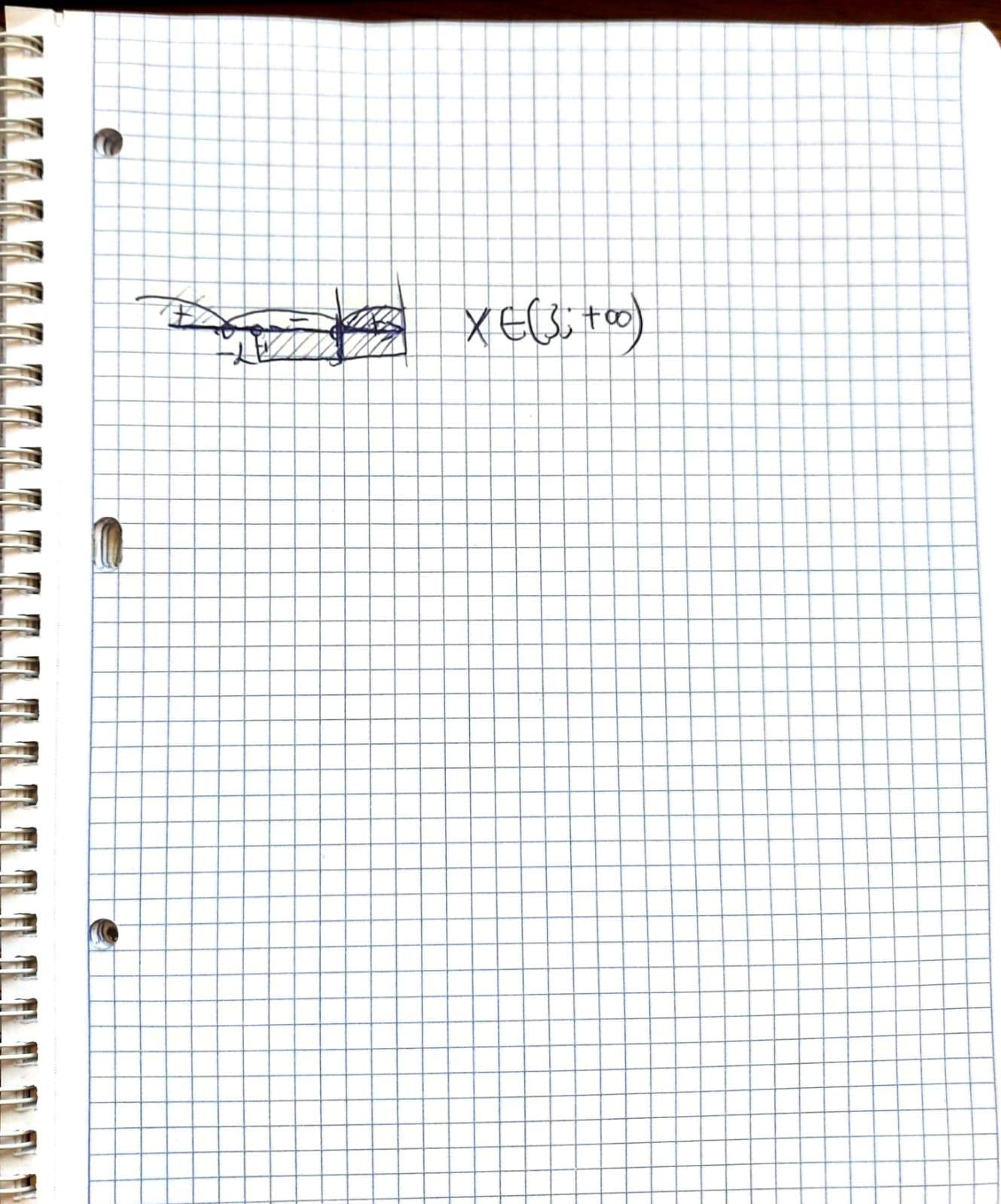
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: jinadria
Предмет: Окружающий мир,
автор: games557
Предмет: Геометрия,
автор: alkarpov79oyxuv7
Предмет: Психология,
автор: DashaFig