Question

Очень срочно, пожалуйста

Answer 1

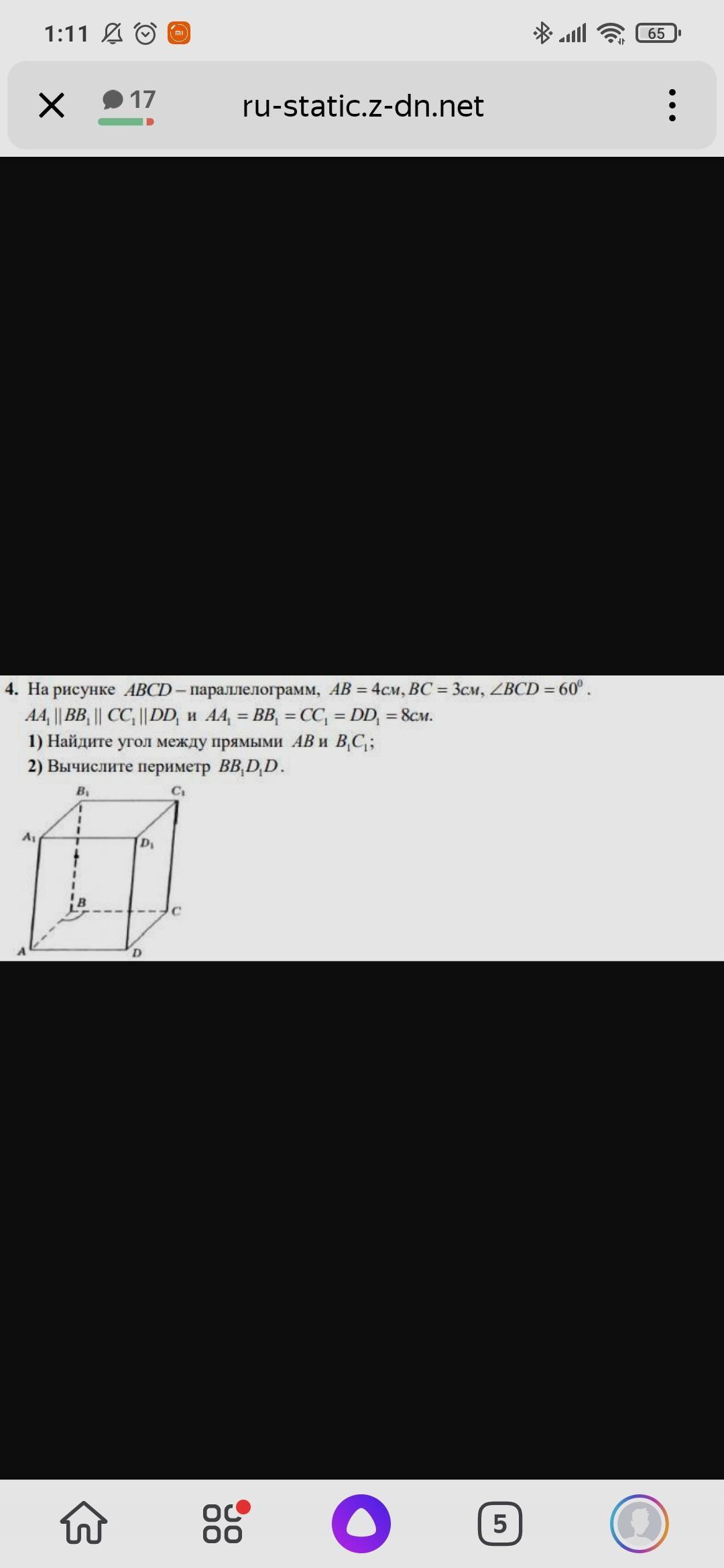
На рисунке АВСD- параллелограмм , АВ=4 см , ВС=3 см, ∠ВСD=60°. АА₁||BB₁||CC₁||DD₁ , АА₁=BB₁=CC₁=DD₁=8 см .Найдите а) угол между прямыми АВ и В₁С₁ ;б) периметр ВDD₁B₁ .

Объяснение:

а)  

• ВВ₁С₁С- параллелограмм , по признаку параллелограмма о 2-х равных и параллельных сторонах BB₁||CC₁ и BB₁=CC₁ ⇒B₁C₁ || ВС.

• АВВ₁А₁- параллелограмм , по признаку параллелограмма о 2-х равных и параллельных сторонах АА₁||ВВ₁ и АА₁=ВВ₁ ⇒А₁В₁ || АВ.

• Плоскости (АВС) ||(А₁B₁C₁)  по признаку параллельности 2-х плоскостей , тк B₁C₁ || ВС , А₁В₁ || АВ. Тогда углом между прямыми АВ и В₁С₁ будет угол между СD и СВ , те ∠ВСD=60°.

б)  ВDD₁B₁-параллелограмм  , Р(ВDD₁B₁)=2*(BD+DD₁) .

Из ΔBDC , по т. косинусов  BD²=CD²+CB²-2*CD*CB*cos∠BCD,

BD=√(4²+3²-2*4*3*cos 60°)=√13.  Р(ВDD₁B₁)=2*(√13+8) (см).