Помогите пожалуйста)

Ответы
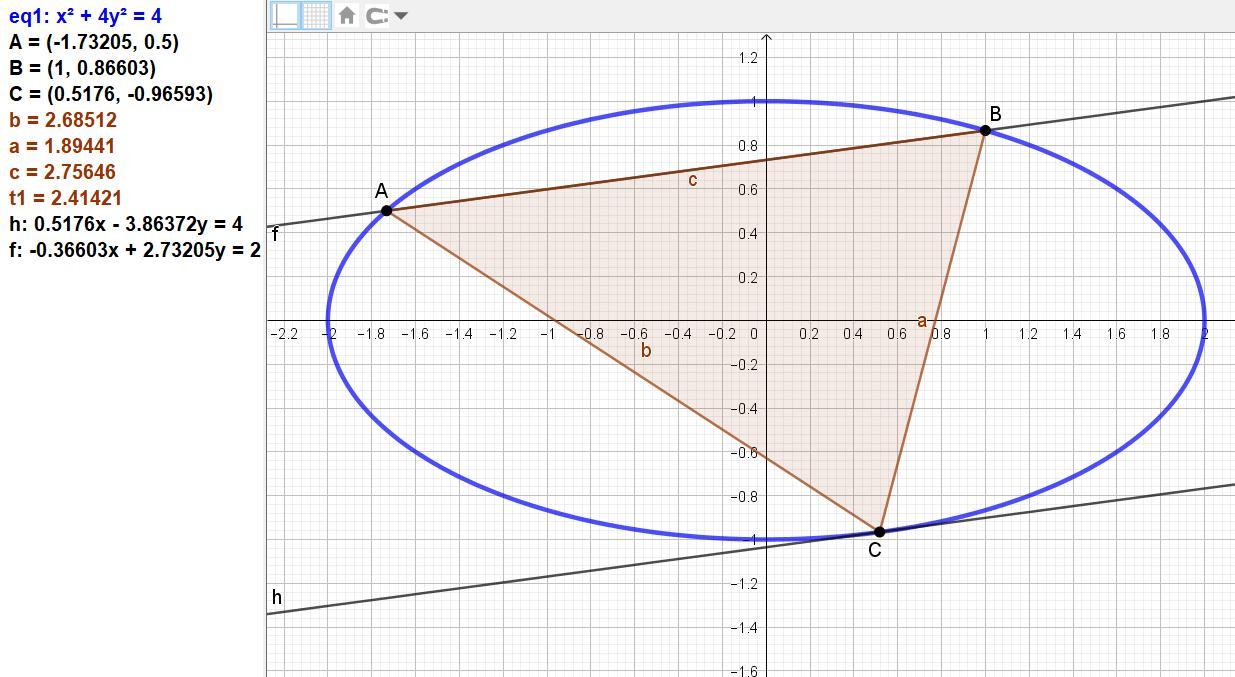
На эллипсе x² + 4y² = 4 даны 2 точки: А(-√3; (1/2)) и В(1; (√3/2)).
Примем третью точку треугольника на этом же эллипсе С(x; y).
Площадь треугольника по координатам выражается формулой:
S = (1/2) |(x(A) - x) (y(A) - y)|
|(x(B) - x) (y(B) - y)|.
Подставим известные координаты точек А и В.
S = (1/2) (-√3 - x)((√3/2) - y) - ((1/2) - y)(1 - x).
После упрощения получаем:
S = ((1 -√3 )/4)x + ((1 +√3)/2)y - 1.
Выразим уравнение эллипса через переменную x.
y = +-√(4 - x²)/2, но так как точка С в треугольнике с максимальной площадью лежит в отрицательной полуплоскости, то для неё принимаем y = -√(4 - x²)/2 и подставляем в полученное уравнение площади.
S = ((1 -√3 )/4)x + ((1 +√3)/2)(-√(4 - x²)/2) - 1. Раскрыв скобки имеем:
S = ((1 -√3 )/4)x - ((1 +√3)/4)(4 - x²) - 1.
Находим производную этой функции и приравниваем её нулю для определения экстремума.
S' = ((1 + √3)/(4√(4 - x²))x + (1/4)( 1 - √3) = 0.
Результат: х = √(2 - √3) ≈ 0,51764.
Координата у = -(√(2 + √3))/2 ≈ -0,96593.
Ответ: площадь S = 1 + √2 ≈ 2,41421.