Предмет: Геометрия,
автор: ErenAckerman
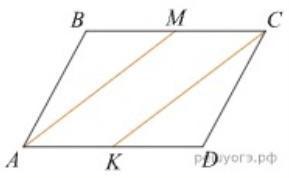
В некотором выпуклом четырёхугольнике проведены биссектрисы противоположных углов. Докажите факт:если биссектрисы противоположных углов четырёхугольника параллельны, то такой четырёхугольник - параллелограмм
Приложения:
vikll:
Если это так, то есть этот четырехугольник является параллелограммом, то его противолежащие углы равны, значит их биссектрисы делят их же на равные углы .
Отложим углы от одной из биссектрис на один градус меньше существующих. В таком случае мы получаем выпуклый четырехугольник в котором биссектрисы углов параллельны(мы не трогали прямые АМ и КС) и у которого противолежащие углы не равны (отличаются на 2-а градуса) значит он не может быть параллелограммом. .
Значит мы не можем доказать факт который от нас требуется доказать . Но можем предположить, что в условии забыли указать равенство этих биссектрис
Ответы
Автор ответа:
0
Сергей сказал чтобы мы решили сами
хааххаа прикинь Сергей зайдёт и увидит у меня это первой вкладкой высветилось
Похожие вопросы
Предмет: Русский язык,
автор: rzn6217
Предмет: Русский язык,
автор: nikitinivan306
Предмет: Английский язык,
автор: vladimirshavand
Предмет: Русский язык,
автор: belstriksa
Предмет: Физика,
автор: dasghii