Предмет: Алгебра,
автор: lerailina047
Дано :
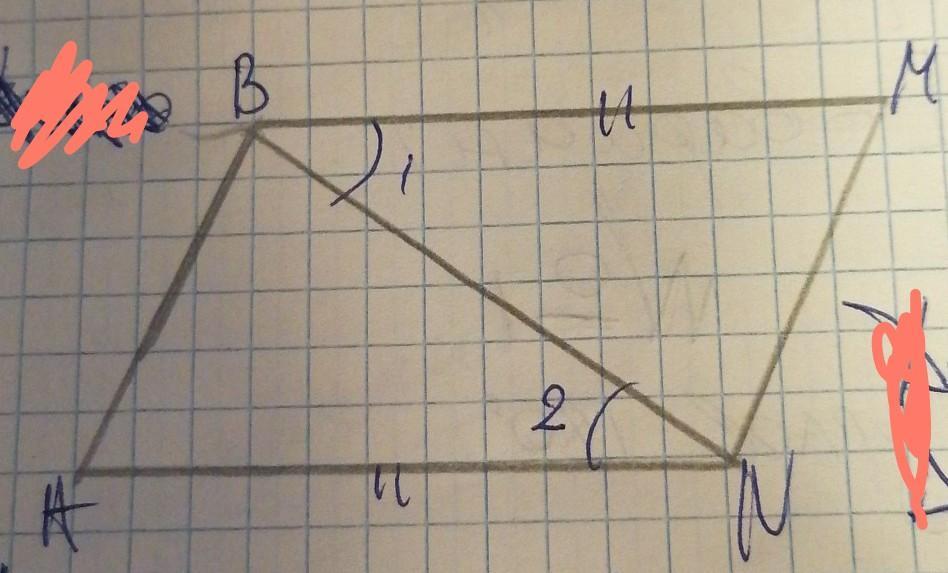
ВМ=АN, угол 1 = углу 2
Доказать :
Треугольник ВМN = треугольнику NАВ
Приложения:
Ответы
Автор ответа:
1
Предположим, что bm||an. Тогда bn - секущая. Угол anb и угол nbm - накрест лежащие. По условию они равны. Из этого следует, что bm действительно параллельно an.
Т.к. bm||an и bn=an, то abmn - параллелепипед, а значит углы ban и bmn равны (исходя из свойств параллелепипеда).
Исходя из свойств суммы углов треугольника, можно сделать вывод, что т.к. оба треугольника имеют 2 одинаковых угла, третий угол, соответственно, так же будет равен.
Значит треугольники равны по стороне bn и прилежащей к ней углам.
Похожие вопросы
Предмет: Английский язык,
автор: rrrrrrrrrrrrrrr3
Предмет: Другие предметы,
автор: z2186845
Предмет: Русский язык,
автор: sofocha112233
Предмет: Музыка,
автор: didanova2004
Предмет: Алгебра,
автор: madeirafunchaligor