Сколькими способами внутри клетчатого прямоугольника ABCD размера 99×100 можно отметить узел клетчатой решётки P (точка на пересечении линий сетки) так, чтобы площади всех четырёх треугольников ABP, BCP, CDP и DAP были равны целым числам?
Ответы
Ответ:
4802 точки.
Объяснение:
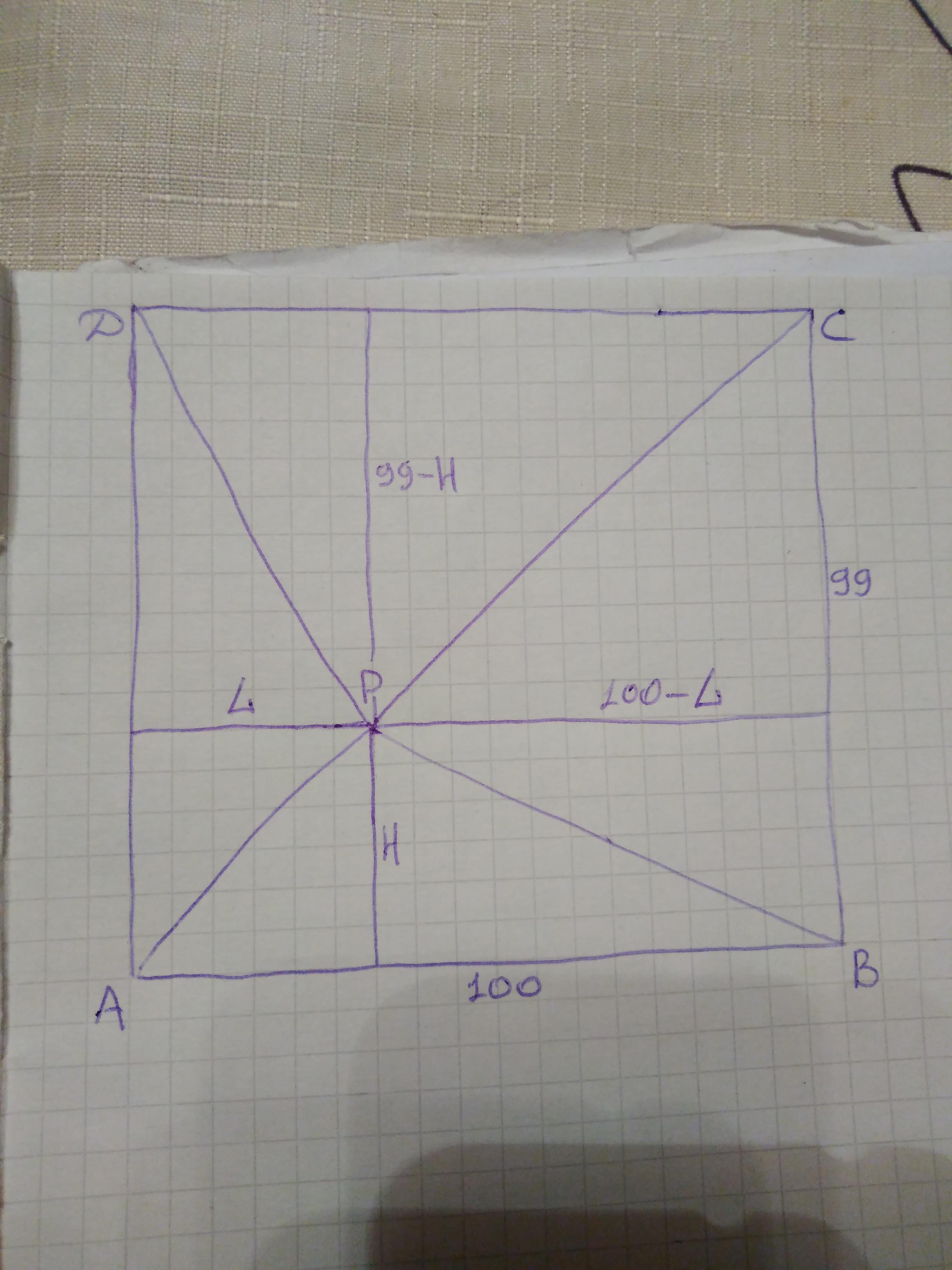
Обозначим углы прямоугольника так, что AB = CD = 100; BC = AD = 99.
Возьмём какую-нибудь точку Р внутри прямоугольника.
Смотрите рисунок.
Посчитаем площади треугольников:
Sтр = a*h/2
Здесь а - основание, h - высота, то есть расстояние от основания до т. Р.
Чтобы площадь треугольника была целой, или а, или h должно быть чётным.
Для ясности обозначим расстояние от AB до P = H, от AD до P = L.
Тогда расстояние от CD до P = 99-H, а от BC до P = 100-L (подумайте, почему так!)
S(ABP) = AB*H/2 = 100H/2 = 50H
S(CDP) = CD*(99-H)/2 = 100(99-H)/2 = 50(99-H)
Эти две площади целые при любом H, то есть при любом положении т. P.
Значит, в этом пункте нет никаких ограничений на положение т. P.
S(ADP) = AD*L/2 = 99L/2
S(BCP) = BC*(100-L)/2 = 99(100-L)/2
Эти две площади будут целыми, только если L и 100-L - чётные числа.
Подходят ряды на расстоянии 2, 4, 6, ..., 98 от стороны AD.
Рядов (98-2)/2 + 1 = 49, и в каждом по 98 точек.
Всего 49*98 = 4900 - 98 = 4802 точки.