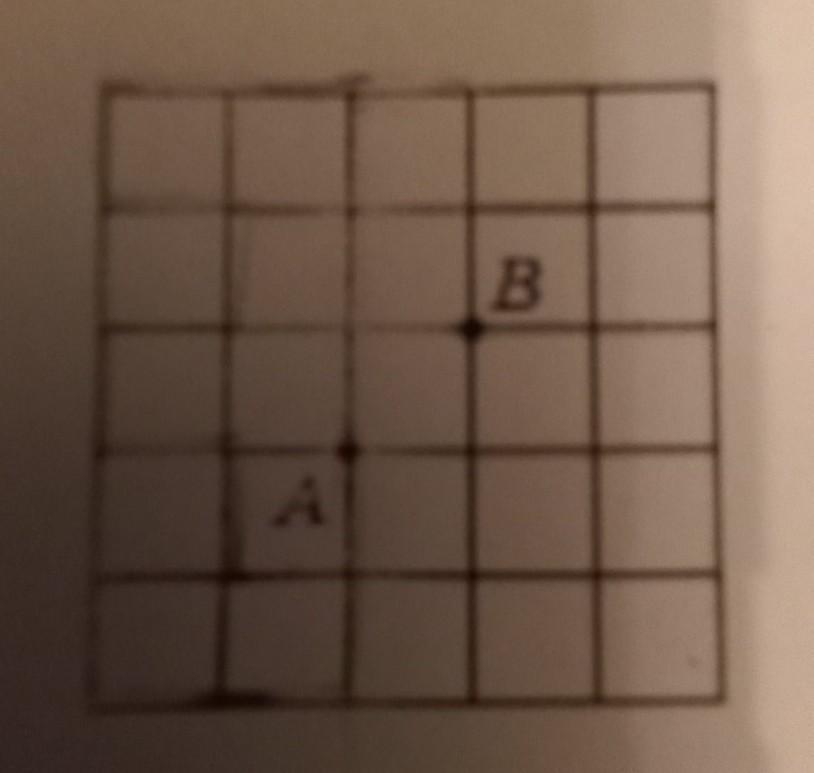
4*. Любознательный турист хочет прогуляться по улицам Старого города от вокзала (точка А на плане) до своего отеля (точка В). Он хочет, чтобы его маршрут был как можно длиннее, но дважды оказываться на одном и том же перекрёстке ему неинтересно, и он так не делает. Нарисуйте на плане самый длинный возможный маршрут и докажите, что более длинного нет.
Ответы
Ответ:
Пример. Один из возможных маршрутов туриста изображён на рисунке слева. Двигаясь по этому пути, турист пройдёт 34 улицы (улицей мы называем отрезок между двумя соседними перекрёстками).
Оценка. Всего в Старом городе 36 перекрёстков. Всякий раз, когда турист проходит очередную улицу, он попадает на новый перекрёсток. Таким образом, больше 35 улиц турист пройти не сможет (начальный перекрёсток A не считается). Покажем, что посетить 35 перекрёстков (и, следовательно, пройти 35 улиц) турист тоже не сможет. Для этого раскрасим перекрёстки в чёрный и белый цвета в шахматном порядке (рис. справа). Всякий раз, проходя улицу, турист попадает на перекрёсток другого цвета. И отель, и вокзал расположены на белых перекрёстках. Поэтому любой маршрут содержит чётное число улиц, а число 35 нечётно.
Пошаговое объяснение: