Предмет: Геометрия,
автор: Samorina
1. В трапеції сума кутів при одній з основ дорівнює 90⁰. Довести, що сума квадратів бічних сторін цієї трапеції дорівнює квадрату різниці її основ.
Ответы
Автор ответа:
2
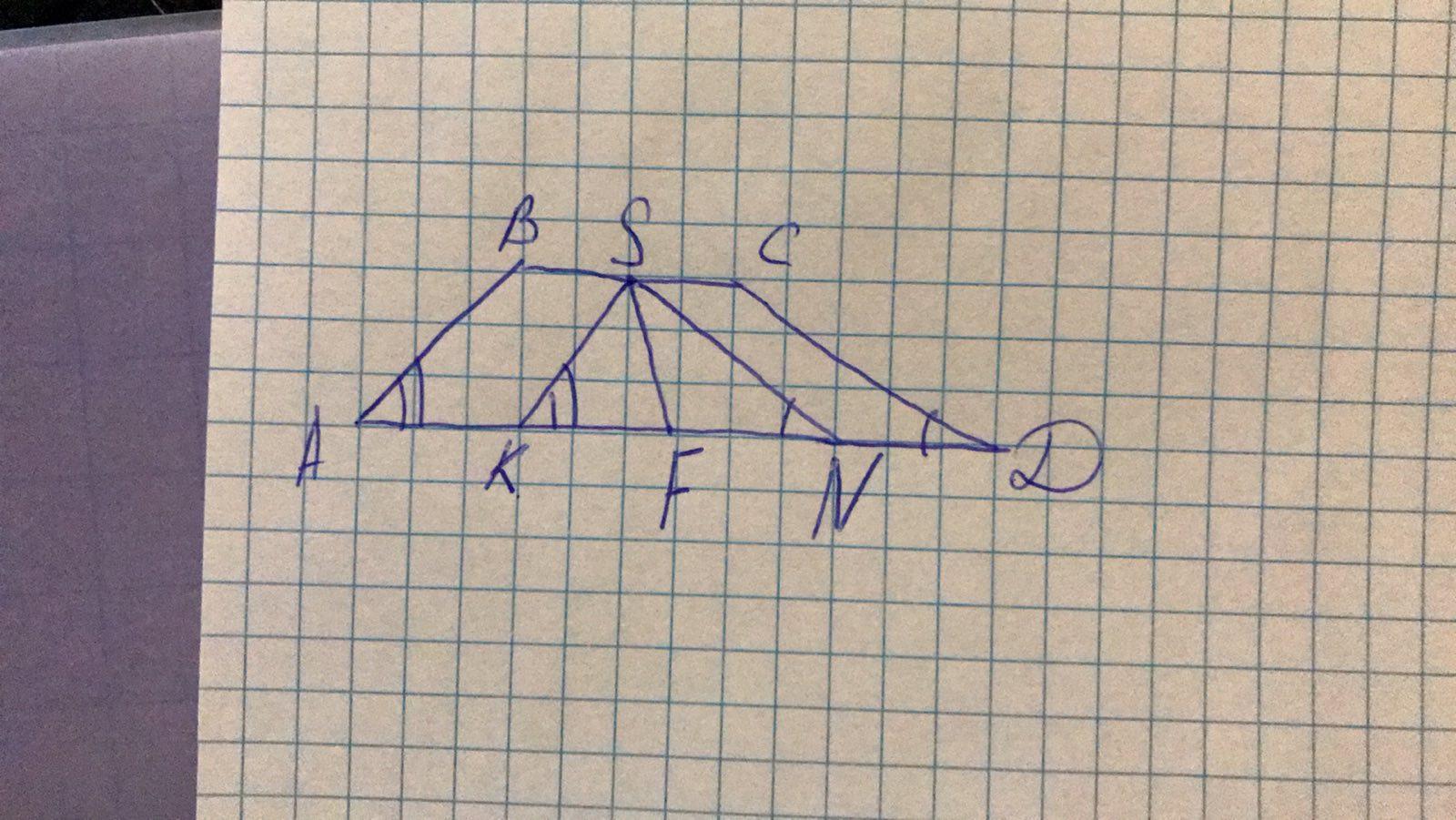
Ответ:2SF=AD-BC
Объяснение: Будуємо трапецію ABCD, За умовою нам дано що кут А+D=90 градусів. Якщо сума кутів при будь-якій основі трапеції дорівнює 90, то відрізок, що з'єднує середини основ, дорівнює їх піврізниці. Креслимо відрізок через середину меншої основи до основи більшої. Назвем його SF. З точки S проведемо прямі паралельні AB і СD. В результаті цього у нас утворююця точки K, N, ці точки є пересічення основи трапеції AD. Тоді кут SKN+SNK=куту A+D= 90 градусів. Тому кут KSN = 90 градусів. Значить FK= AF-AK=AN-BS=DF-CS=DF-DN=FN. Значить SF медіана прямокутного трикутника KSN. Проведена з вершини прямого кута. Тому 2SF = KN = AD - AK - ND = AD - BS - SC = AD - BC.
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: Elena129
Предмет: Русский язык,
автор: leir03
Предмет: Русский язык,
автор: DaRkCat2
Предмет: Литература,
автор: Krasavua
Предмет: Литература,
автор: anilaelims