Предмет: Алгебра,
автор: Аноним
Найти наклонную асимптоту.
Приложения:
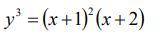
Ответы
Автор ответа:
2
Ответ:
Приложения:
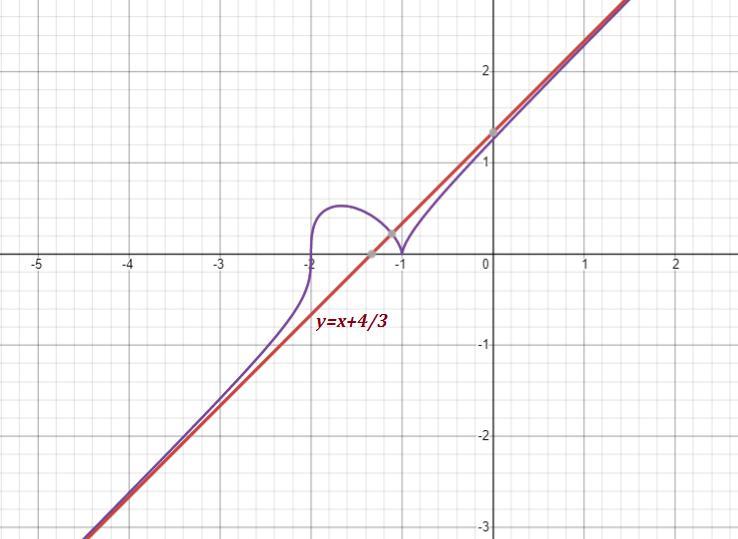
Аноним:
ну просто как этим не гордиться
работа описывает старание
Похожие вопросы
Предмет: Русский язык,
автор: рая1967
Предмет: Русский язык,
автор: zayac1310
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: riabovalia33