Предмет: Математика,
автор: regon598
Найти интеграл......
Приложения:
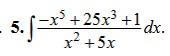
Ответы
Автор ответа:
0
Ответ: -x⁴/4+5x³/3 - 1/5 · ( ln|x+5| -ln x|)+C
Пошаговое объяснение:
∫(-x⁵+25x³+1)dx/(x²+5x) =-∫(x⁵-25x³)dx/x(x+5) + ∫1dx/x(x+5) =
=-∫x³(x²-25)dx/x(x+5) + ∫dx/x(x+5) =-∫x³(x-5)(x+5)dx/x(x+5) + ∫dx/x(x+5) =
= -∫x²(x-5)dx + ∫dx/x(x+5) =-∫(x³-5x²)dx + ∫dx/x(x+5) =-x⁴/4+5x³/3 + ∫dx/x(x+5)
Вычислим отдельно ∫dx/x(x+5) = ∫dx/x²(1+5/х) =
| пусть 1+5/х=t, тогда -5dx/х²=dt , dx= -5dt/x² | =-1/5 ·∫dt/t= -1/5 · ln|t| +C=
= -1/5 · ln|1+5/x| +C = -1/5 · ln|(x+5)/x| +C= -1/5 · ( ln|x+5| -ln x|)+C
⇒ ∫(-x⁵+25x³+1)dx/(x²+5x)= -x⁴/4+5x³/3 - 1/5 · ( ln|x+5| -ln x|)+C
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: enotikcom12
Предмет: Русский язык,
автор: школьник398
Предмет: Литература,
автор: elyaket1