Предмет: Алгебра,
автор: Аноним
Вычислить двойной интеграл по области D,ограниченной линиями.
Приложения:
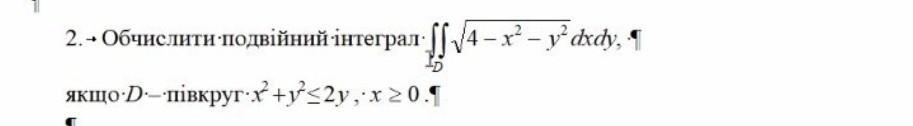
yugolovin:
x^2+(y-1)^2=1 - окружность с центром в точке (0;1) и радиусом 1; x>0 - то есть правая половина круга. Переходите к полярным координатам.
Прошу прощения, времени на ответ нет
Ответы
Автор ответа:
2
Ответ:
- это круг , центр которого находится в точке (0,1) , радиус равен R=1 .
Так как задано неравенство , то область D - это полукруг, который находится в правой полуплоскости .
Перейдём к полярным координатам : .
Запишем уравнение окружности, ограничивающей заданный полукруг, в полярных координатах .
Приложения:


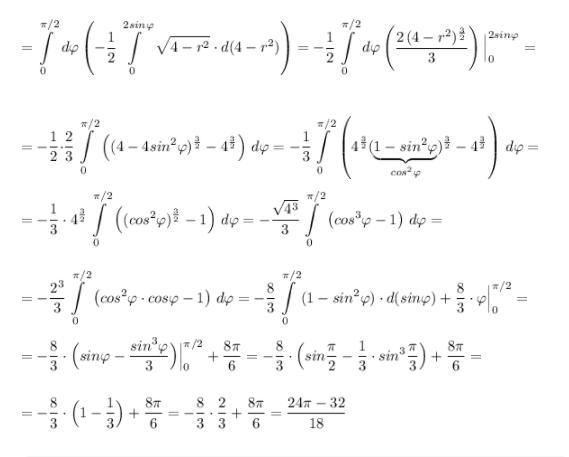
см скрин
Похожие вопросы
Предмет: Қазақ тiлi,
автор: 10минутсыз7
Предмет: Русский язык,
автор: блабла32
Предмет: Русский язык,
автор: заголовокктексту
Предмет: Математика,
автор: MAXIMUM36
Предмет: Русский язык,
автор: qehramanovpdpece