Предмет: Алгебра,
автор: asminarezepova045
2.13. Решите уравнение: алгебра 8 класс номер 2.13
Приложения:
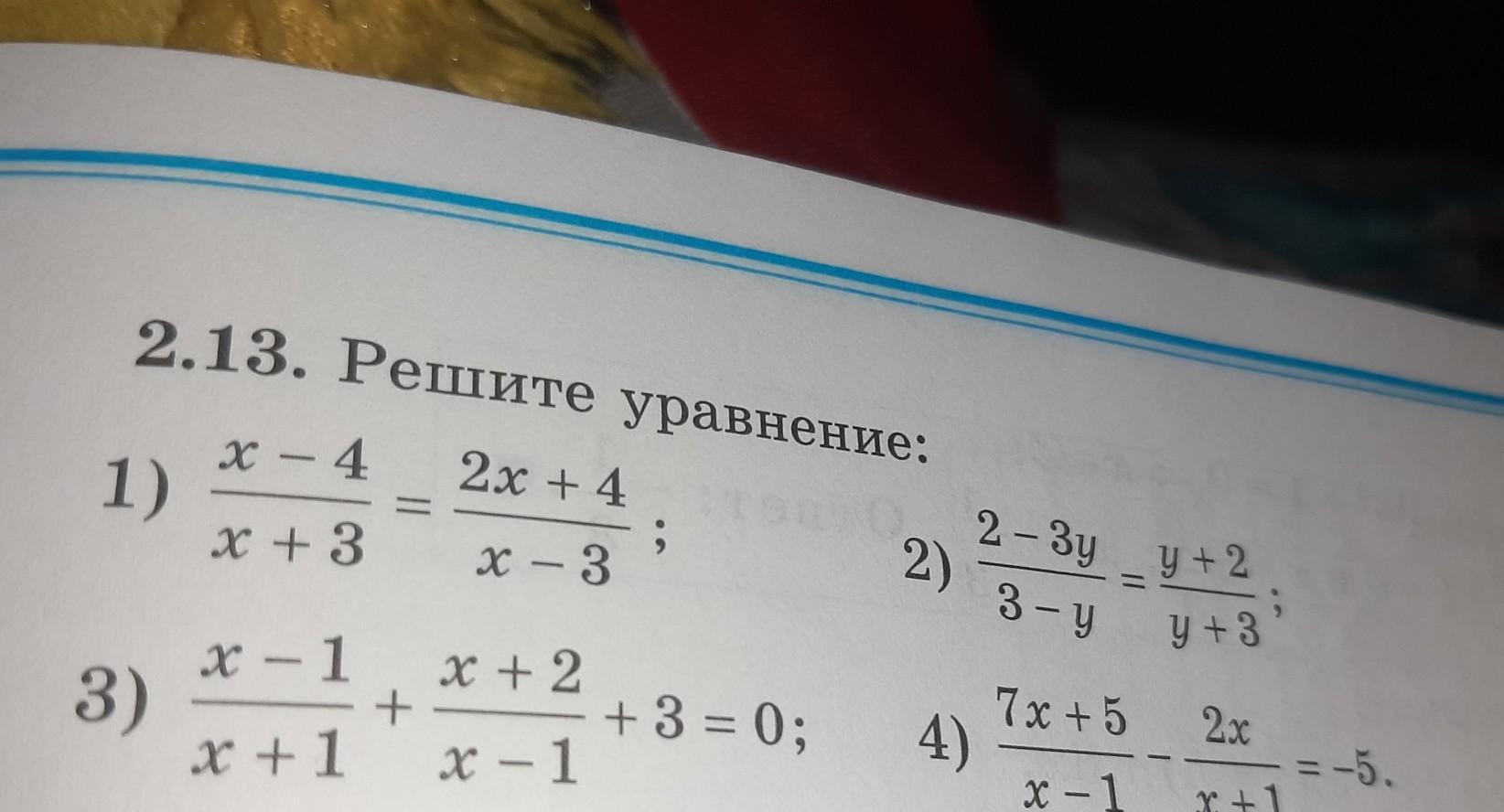
Ответы
Автор ответа:
2
1)
ОДЗ:
,
;
Ответ: ;
2)
ОДЗ:
,
;
Ответ: ;
3)
ОДЗ:
,
;
Ответ: ;
4)
ОДЗ:
,
;
Ответ: ;
Похожие вопросы
Предмет: Окружающий мир,
автор: zyzi1
Предмет: Українська мова,
автор: vsenya
Предмет: Русский язык,
автор: юlьчик
Предмет: Информатика,
автор: sergey000popov