Предмет: Алгебра,
автор: danil34215123
даю 30 баллов. Нужно срочно решить!
Приложения:
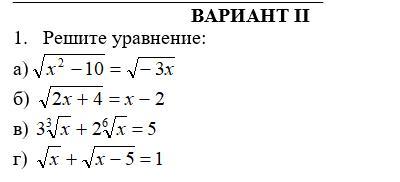
Ответы
Автор ответа:
1
Объяснение:
Т.к. степень в ур-нии равна = 1/6 и свободный член = -5/3 < 0, значение действительных решений у соответствующего уравнения не существует.
Приложения:

danil34215123:
Где г?
нашел, не заметил
г сейчас напишу
Похожие вопросы
Предмет: Окружающий мир,
автор: Diana4711
Предмет: Русский язык,
автор: nastyarushe
Предмет: Английский язык,
автор: EdinoroGeck
Предмет: Английский язык,
автор: fbhikhfdik
Предмет: Физика,
автор: mmnnbb66