Предмет: Геометрия,
автор: kyotami
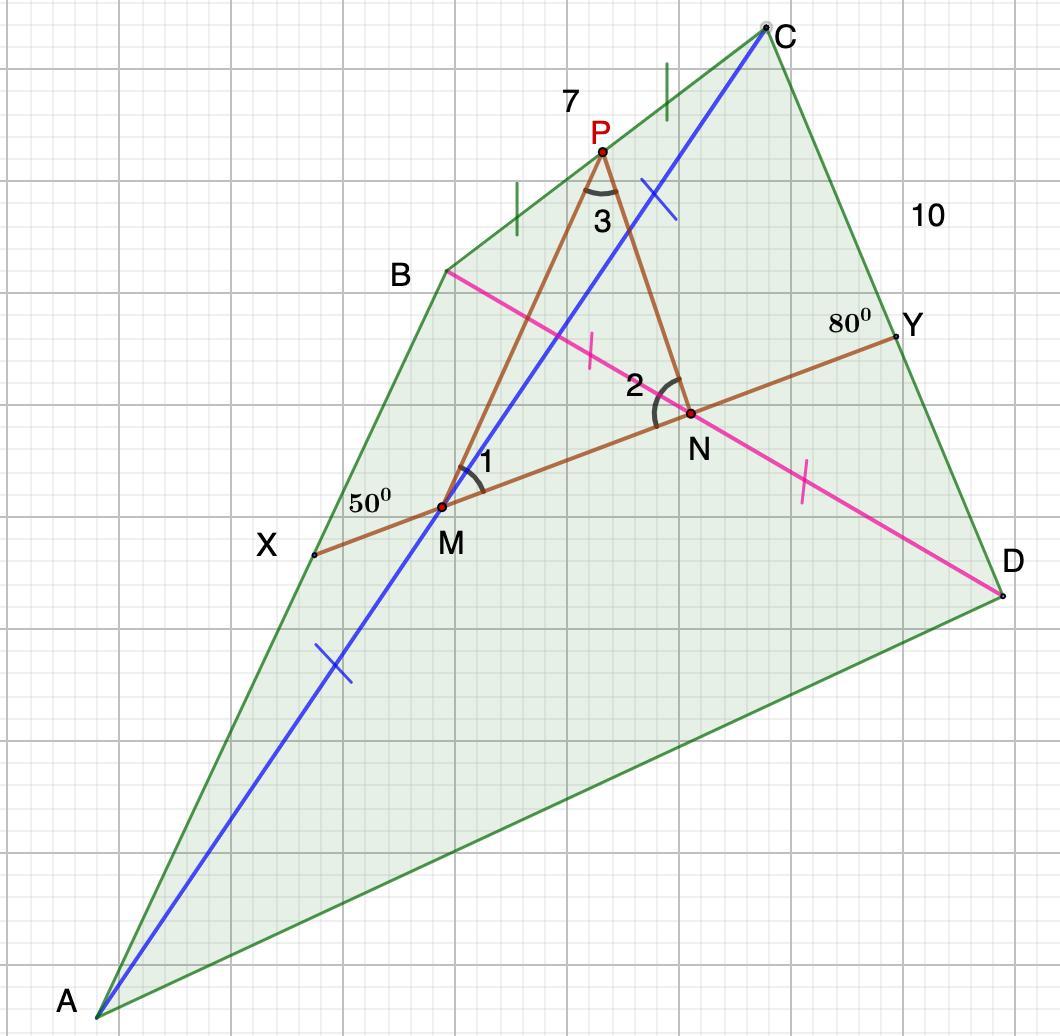
Прямая, проходящая через середины M и N диагоналей четырёхугольника ABCD, пересекает стороны AB и CD в точках X и Y соответственно и образует со сторонами четырёхугольника углы ∠BXM = 50° и ∠CYN = 80°. Найдите MN, если BC = 7, CD = 10
cos20093:
Интересно, что условие этой задачи можно сильно
"обкрамсать". Не имеет значения, чему именно равны углы и BC. В разумных пределах, конечно, то есть конструкция должна существовать. Тогда, если E - точка пересечения AB и DC, то единственно, что важно - что EY = XY (в данном случае это следует из величин углов). Тогда MN = CD/2.
Пример условия, на котором можно провалить любого на экзамене. Не потому, что задача сложная - она элементарная. Но в условие есть сильное отвлечение. Я два дня потратил, пытаясь понять, как тут задействованы углы и величина BC. Причем я сразу понял, что EYX - равнобедренный. И - все равно, ковырялся кучу времени - никакой экзамен столько не длится. Только когда провел через M и N прямые параллельно AD, мгновенно все увидел. Чистая психология, никакой геометрии.
Ответы
Автор ответа:
2
Ответ:
5 ед.
Объяснение:
Дано: ABCD - четырехугольник;
АС и ВD - диагонали.
АМ = МС; BN = ND;
∠BXM = 50° ; ∠CYN = 80°;
BC = 7, CD = 10
Найти: MN.
Решение:
Отметим точку Р - середину отрезка ВС и соединим ее с точками М и N.
1. Рассмотрим ΔBCD.
BP = PC (построение)
BN = ND (условие)
⇒ NP - средняя линия ΔBCD.
- Средняя линия треугольника параллельна основанию и равна его половине.
⇒ NP || CD;
.
NP = 10 : 2 = 5
2. Рассмотрим ΔАВС.
BP = PC (построение)
АМ = МС (условие)
⇒ МР - средняя линия ΔBCD.
МР || АВ.
3. Рассмотрим ΔМРN.
∠1 = ∠ВХМ =50° (соответственные при АВ || МР и секущей ХY)
∠2 = ∠CYN = 80° (соответственные при NP || CD и секущей ХY)
- Сумма углов треугольника равна 180°.
⇒ ∠3 = 180° - ∠1 - ∠2 = 50°.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
⇒ ΔМРN - равнобедренный.
МN = NP = 5.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: aleksandrtimof1
Предмет: Русский язык,
автор: Даниилка2005
Предмет: Русский язык,
автор: Demaster87
Предмет: Математика,
автор: fucgbvhbvg
Предмет: Математика,
автор: aleksandra5813