Question

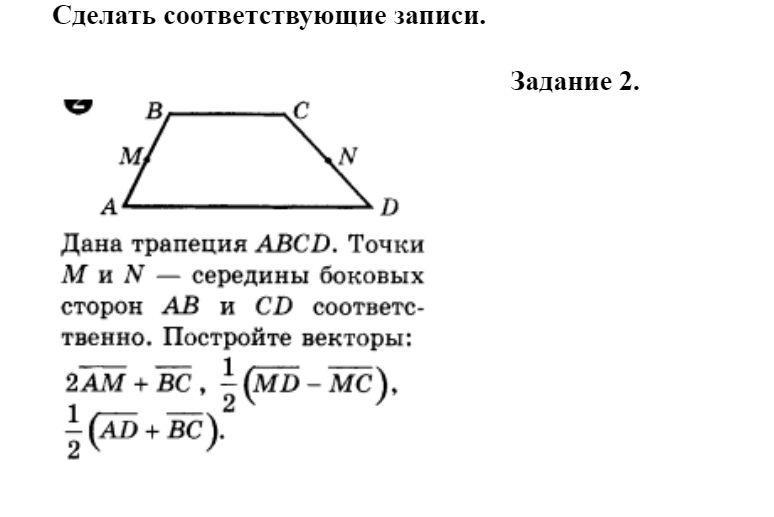
Дана трапеция ABCD. Точки M и N - середины боковых сторон AB и CD соответственно. Постройте векторы: 2AM+ BC, 1/2(AD-MC), 1/2(AD+BC)²

Answer 1

Ответ:

Ре­ше­ние.

a) По усло­вию, четырёхуголь­ник PBCQ впи­сан­ный. Зна­чит, \angle BCQ плюс \angle BPQ =180 гра­ду­сов. От­ре­зок MN — сред­няя линия тра­пе­ции ABCD, она па­рал­лель­на ос­но­ва­нию BC, а тогда \angle BCQ плюс \angle QNM =180 гра­ду­сов как од­но­сто­рон­ние углы при па­рал­лель­ных пря­мых. Сле­до­ва­тель­но, \angle BPQ =\angle QNM. Для смеж­ных углов спра­вед­ли­во ра­вен­ство \angle BPQ плюс \angle MPQ=180 гра­ду­сов, а зна­чит, \angle QNM плюс \angle MPQ=180 гра­ду­сов. В четырёхуголь­ни­ке MPQN сумма про­ти­во­по­лож­ных углов равна 180°, по­это­му во­круг него можно опи­сать окруж­ность. Тем самым, точки M, N, P и Q лежат на одной окруж­но­сти, что и тре­бо­ва­лось до­ка­зать.

б) Пусть \angle QNM = \angle QDA= альфа (эти углы равны как со­от­вет­ствен­ные углы при па­рал­лель­ных пря­мых). В пунк­те а) было по­ка­за­но, что \angle QNM плюс \angle MPQ=180 гра­ду­сов, это озна­ча­ет, что \angle QDA плюс \angle MPQ=180 гра­ду­сов, и, сле­до­ва­тель­но, точки A, D, P и Q тоже лежат на одной окруж­но­сти.

Впи­сан­ные углы, опи­ра­ю­щи­е­ся на одну и ту же дугу окруж­но­сти, равны. Сле­до­ва­тель­но, \angle PBQ = \angle PCQ и \angle PAQ = \angle PDQ . Зна­чит, тре­уголь­ни­ки DPC и AQB по­доб­ны по двум углам. Сле­до­ва­тель­но, \angle AQB = \angle DPC = 90 гра­ду­сов, так как по усло­вию DP и PC пер­пен­ди­ку­ляр­ны.

В пря­мо­уголь­ном тре­уголь­ни­ке AQB точка M − се­ре­ди­на ги­по­те­ну­зы. Сле­до­ва­тель­но, MQ= AM=MB= дробь, чис­ли­тель — AB, зна­ме­на­тель — 2 = дробь, чис­ли­тель — 21, зна­ме­на­тель — 2 =10,5. С дру­гой сто­ро­ны, сред­няя линия тра­пе­ции MN = дробь, чис­ли­тель — AD плюс BC, зна­ме­на­тель — 2 = дробь, чис­ли­тель — 4 плюс 17, зна­ме­на­тель — 2 =10,5. Зна­чит, тре­уголь­ник NMQ рав­но­бед­рен­ный и в нём QN= 2 умно­жить на MN умно­жить на ко­си­нус альфа = 21 ко­си­нус альфа . Оста­лось найти ко­си­нус угла CDA.

Для этого на от­рез­ке AD от­ме­тим точку E, так что AE=BC=4, тогда DE=13, CE=21. Для тре­уголь­ни­ка CDE за­пи­шем тео­ре­му ко­си­ну­сов: CE в сте­пе­ни 2 =DE в сте­пе­ни 2 плюс CD в сте­пе­ни 2 минус 2DE умно­жить на CD умно­жить на ко­си­нус альфа , от­ку­да вы­ра­зим ко­си­нус угла CDE:

ко­си­нус альфа = дробь, чис­ли­тель — DE в сте­пе­ни 2 плюс CD в сте­пе­ни 2 минус CE в сте­пе­ни 2 , зна­ме­на­тель — 2DE умно­жить на CD = дробь, чис­ли­тель — 13 в сте­пе­ни 2 плюс 20 в сте­пе­ни 2 минус 21 в сте­пе­ни 2 , зна­ме­на­тель — 2 умно­жить на 13 умно­жить на 20 = дробь, чис­ли­тель — 16, зна­ме­на­тель — 65 .

Итак,

QN=21 ко­си­нус альфа =21 умно­жить на дробь, чис­ли­тель — 16, зна­ме­на­тель — 65 = дробь, чис­ли­тель — 336, зна­ме­на­тель — 65 .

При­ве­дем дру­гое ре­ше­ние пунк­та б):

За­ме­тим, что раз тре­уголь­ник PDC — пря­мо­уголь­ный, то PN = CN = ND = 10, MN= дробь, чис­ли­тель — 17 плюс 4, зна­ме­на­тель — 2 =10,5 — сред­няя линия тра­пе­ции ABCD. Зная бо­ко­вые сто­ро­ны и ос­но­ва­ния тра­пе­ции, не­труд­но найти ее вы­со­ту из тре­уголь­ни­ка CED со сто­ро­на­ми 21, 20 и 13: h= дробь, чис­ли­тель — 252, зна­ме­на­тель — 13 . От­сю­да най­дем синус \angle BAD= дробь, чис­ли­тель — дробь, чис­ли­тель — 252, зна­ме­на­тель — 13 , зна­ме­на­тель — 21= дробь, чис­ли­тель — 12, зна­ме­на­тель — 13 , синус \angle CDA= дробь, чис­ли­тель — дробь, чис­ли­тель — 252, зна­ме­на­тель — 13 , зна­ме­на­тель — 20= дробь, чис­ли­тель — 63, зна­ме­на­тель — 65 . Те­перь, так как \anglePMN=\angleBAD, по тео­ре­ме си­ну­сов для тре­уголь­ни­ка MPN, можем найти ра­ди­ус окруж­но­сти, опи­сан­ной около MPQN:

R= дробь, чис­ли­тель — PN, зна­ме­на­тель — 2 синус \anglePMN = дробь, чис­ли­тель — 10, зна­ме­на­тель — 2 умно­жить на дробь, чис­ли­тель — 12 13, зна­ме­на­тель — = дробь, чис­ли­тель — 65, зна­ме­на­тель — 12 .

Так как \angleQNM=\angleCDA, най­дем MQ по тео­ре­ме си­ну­сов для тре­уголь­ни­ка MQN:

MQ=2R синус \angleQNM=2 умно­жить на дробь, чис­ли­тель — 65, зна­ме­на­тель — 12 умно­жить на дробь, чис­ли­тель — 63, зна­ме­на­тель — 65 = дробь, чис­ли­тель — 21, зна­ме­на­тель — 2 .

Таким об­ра­зом, тре­уголь­ник MQN — рав­но­бед­рен­ный:

QN=2 умно­жить на MN умно­жить на ко­си­нус \angleMNQ=2 умно­жить на дробь, чис­ли­тель — 21, зна­ме­на­тель — 2 умно­жить на ко­рень из 1 минус левая круг­лая скоб­ка дробь, чис­ли­тель — 63, зна­ме­на­тель — 65 пра­вая круг­лая скоб­ка в сте­пе­ни 2 =

=21 умно­жить на дробь, чис­ли­тель — ко­рень из 65 в сте­пе­ни 2 минус 63 в сте­пе­ни 2 , зна­ме­на­тель — 65 = дробь, чис­ли­тель — 21, зна­ме­на­тель — 65 ко­рень из 2 умно­жить на 128= дробь, чис­ли­тель — 21 умно­жить на 16, зна­ме­на­тель — 65 = дробь, чис­ли­тель — 336, зна­ме­на­тель — 65 .

Ответ: б) дробь, чис­ли­тель — 336, зна­ме­на­тель — 65 .