Question

довести що бісектриси трикутника не можуть перетинатися під прямим кутом​

Answer 1

Ответ:

Пошаговое объяснение:

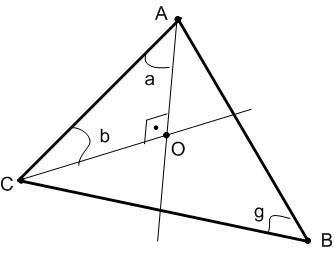
Дан ΔABC. Построим биссектрисы углов А и C. Они пересекутся в точке О. Теперь предположим, что угол пересечения биссектрис равен 90°: ∠AOC=90°. Тогда:

рассмотрим ΔACO. Угол ∠AOC - прямой (по предположению), следовательно ∠a+∠b=180 - ∠AOC; ∠a+∠b=90° или проще запишем        a+b=90°  (1)

Но ∠a=∠BAC/2 ∠b=∠ACB/2 (по определению биссектрис углов), следовательно:

2a+2b+g=180°;

a+b=(180-g)/2;

a+b=180/2-g/2;

a+b=90-g/2   (2)

но, предполагая, что угол между биссектрисами равен 90°, мы получили соотношение (1) углов a и b вот такое: a+b=90°.

Т.е. соотношение (1) противоречит соотношению (2). Следовательно наше начальное предположение не верно!

Ч.т.д.